Лекция 6: Некоторые задачи нелинейного программирования и нахождение опорного плана для задачи линейного программирования
Алгоритм. Пример
Выше фактически уже описан алгоритм нахождения хотя бы одной вершины многогранника допустимых решений. Сведем вместе все необходимые построения.
Алгоритм.
- Определим направление возрастания целевой функции и выделим грани многогранника допустимых решений, образующие верхнюю (нижнюю) его поверхность. Дополним ее возможными гранями — координатными плоскостями.
- Составим матрицу S косинусов углов между всеми нормалями к действительным и возможным граням сформированной поверхности многогранника допустимых решений.
- Если число r действительных граней верхней (нижней) поверхности не меньше n — размерности задачи, выполняем первый этап алгоритма, исключив из рассмотрения строки и столбцы матрицы S, соответствующие координатным плоскостям.
- Этот пункт является общим для первого и второго этапов. Выбрав произвольно грань или организовав перебор всех граней, или организовав параллельный анализ всех граней, выберем в соответствующей этой грани строке матрицы S n максимальных косинусов. В этой последовательности косинусов, кроме максимального косинуса угла между нормалью выбранной грани и ею же самой, не должно быть косинусов, равных 1 или -1. Таким образом, окажутся выделенными n возможных образующих некоторой вершины многогранника допустимых решений.
- Решаем совместно уравнения выделенных граней.
- Если решение существует и оно неотрицательно, произведем анализ: удовлетворяет ли найденная точка всем ограничениям задачи? Если удовлетворяет, точка действительно является вершиной многогранника. В противном случае необходимо продолжить анализ граней, то есть строк матрицы S.
- Если перебор всех строк матрицы S не привел к успеху на первом этапе выполнения алгоритма, переходим ко второму этапу, введя в рассмотрение координатные плоскости, т.е. начинаем анализ матрицы в полном объеме. Если успех не был достигнут на втором этапе, то, как указано ниже, можно испытать удачу на другой — нижней (верхней) поверхности многогранника допустимых решений. Ведь важно найти хоть какую-то вершину, пусть не столь близкую к вершине-решению. Если мы и теперь не достигли успеха…
В рассматриваемом примере верхнюю поверхность (где следует искать решение) образуют грани (6.6). Поскольку переименование малого количества граней в соответствии с (6.7) не имеет смысла, составим для этих граней и их нормалей таблицу, включающую матрицу косинусов углов между нормалями. Соответствующие косинусы считаем по (6.9) и (6.10), таблицу строим по образу таблицы 6.1. Матрица S в таблице выделена.
Реализуем первый этап алгоритма поиска вершины, исключив из рассмотрения три последние строки и столбцы.
Выберем грань q1. Максимальные косинусы соответствующей (первой) строки матрицы S указывают на систему граней {q1, q2, q3}. Решаем уравнения граней совместно и проверяем решение на выполнение всех неиспользованных ограничений задачи. Получаем вершину E(13, 8, 4).
| Грань | Нормаль | N1 | N2 | N3 | N4 | N5 | N7 | N8 | N9 |
|---|---|---|---|---|---|---|---|---|---|
| q1 | N1 | l | 0,59 | 0,59 | 0,067 | 0,171 | 0,026 | 0,09 | -0,99 |
| q2 | N2 | 0,59 | 1 | 0,9 | -0,43 | -0,29 | -0,56 | 0,625 | -0,56 |
| q3 | N3 | 0,59 | 0,9 | 1 | -0,25 | -0,125 | -0,28 | 0,46 | -0,84 |
| q4 | N4 | 0,067 | -0,43 | -0,25 | 1 | 0,99 | -0,16 | -0,975 | -0,16 |
| q5 | N5 | 0,171 | -0,29 | -0,125 | 0,99 | 1 | -0,27 | -0,92 | -0,27 |
| q7 | N7 | 0,026 | -0,56 | -0,28 | -0,16 | -0,27 | 1 | 0 | 0 |
| q8 | N8 | 0,09 | 0,625 | 0,46 | -0,975 | -0,92 | 0 | 1 | 0 |
| q9 | N9 | -0,99 | -0,56 | -0,84 | -0,16 | -0,27 | 0 | 0 | 1 |
Выберем грань q2. Максимальные косинусы второй строки матрицы указывают на систему граней {q2, q3, q1}, что соответствует уже найденной вершине.
Для грани q3 получаем ту же систему образующих граней, т.е. ту же вершину E.
По строке табл. 6.4 (матрицы S ), соответствующей q4, находим систему {q1, q4, q5}, решением которой является вершина L{6, 10, 4}.
Анализируя строку грани q5, вновь получаем ту же вершину.
Таким образом, мы добились успеха без рассмотрения координатных плоскостей. Однако для полноты анализа исследуем матрицу S полностью.
Анализ строк 1, 3, 4, 5 порождает те же результаты. Максимальные косинусы второй строки, соответствующей грани q2, указывают на систему {q2, q3, q8}. Решаем уравнения совместно и проверяем выполнение всех неиспользованных ограничений. Получаем вершину D(6, 0, 2).
Со строкой, соответствующей q7, начинаются трудности, обусловленные следующими факторами:
- Координатная плоскость — возможная, но не действительная грань.
- Именно нормали к координатным плоскостям образуют угол
 . Нулевое значение этого косинуса неоднозначно
соответствует углам
. Нулевое значение этого косинуса неоднозначно
соответствует углам  и
и  . Поэтому
невозможно правильно упорядочить углы по неубыванию, используя
отрицательные и нулевые значения косинусов.
. Поэтому
невозможно правильно упорядочить углы по неубыванию, используя
отрицательные и нулевые значения косинусов.
Если, не зная, что делать с нулями, упорядочить только косинусы углов между нормалью к q7 (x = 0) и нормалями к граням-границам, то первые три косинуса невозрастающей последовательности укажут на грани {q1, q4, q7}. Однако точка (0, 11, 4) — решение этой системы — не является вершиной многогранника R, так как не удовлетворяет ограничению q6.
Для возможной грани q8, также не обращая внимание на нули,
находим систему {q2, q3, q8}, решением которой является
вершина D(6, 0, 2). (По-видимому, углы между нормалями не вышли из
диапазона ![[0, \pi ]](/sites/default/files/tex_cache/309631c1b5a36e70cf150aafee847785.png) ).
).
По последней строке, соответствующей возможной грани q9, находим систему {q4, q5, q9}, решением которой является вершина K(10, 10, 0).
(Неслучайность успеха в последних трех случаях нуждается в обосновании.)
Отметим, что нет гарантии получения всех вершин поверхности. Ведь группируя вместе грани, мы отдаем предпочтение вершинам с "пологими" склонами, выбирая максимальные значения косинусов. В частности, мы ни разу здесь не получили вершину F(17, 8, 0), в которой целевая функция принимает максимальное значение. Так что второй этап решения задачи ЛП неизбежен. Более того, необходимо не качественное, а аналитическое доказательство того, что рассмотренным путем при выполнении определенных условий будет получена хотя бы одна вершина многогранника R допустимых решений задачи. То есть необходимо доказать теорему существования.
Развитие стратегии решения задачи ЛП
- Выделяя на многограннике R допустимых решений верхнюю и
нижнюю поверхности, мы на деле не столько стремимся "подобраться"
поближе к вершине-решению, сколько стремимся расчленить задачу,
локализовать поиск опорного плана. Если мы с помощью указанных
косинусов начнем исследовать совместно всю совокупность граней
многогранника, то окажемся во власти неразрешимых коллизий. Ни о каком
упорядочении углов в этом случае не может быть речи, так как во всем
диапазоне
![[0, 2\pi ]](/sites/default/files/tex_cache/5cdd10785917606fae8587e609f9d551.png) изменения углов между нормалями к граням
косинус
никогда не даст однозначного ответа об отношении между этими углами.
изменения углов между нормалями к граням
косинус
никогда не даст однозначного ответа об отношении между этими углами. - Многогранник R может иметь столь причудливую форму, что знание значения целевой функции в некоторой его вершине нисколько не определяет того, за сколько шагов будет найдена вершина-решение. Например, двигаясь из вершины, в которой значение целевой функции меньше, можно за один шаг второго этапа алгоритма достичь, как смежную, вершину-решение. В то же время, стремясь найти вершину с большим значением целевой функции, можно оказаться в ситуации, когда для достижения вершины-решения потребуется несколько шагов. Это говорит о том, что анализ суммы коэффициентов целевой функции для выбора верхней или нижней поверхности многогранника R не столь важен.
-
Более того, выбранная таким образом поверхность не всегда может привести к успеху.
Например, на рис. 6.6 верхнюю поверхность образуют грань (ребро), противоположная вершине A, и, возможно, координатные плоскости (оси).
Поскольку при анализе этой поверхности другие грани исключены из рассмотрения, то нет системы двух уравнений, результатом решения которой стали бы вершины, образуемые этой гранью. Мы зашли бы в тупик, если бы не позволили себе рассмотреть и другую, нижнюю, поверхность.
Кстати, в нашем примере нижняя поверхность определяется следующим образом:
Qнижн = {q6, q7, q8, q9}.
Составим для нее матрицу S косинусов в составе табл. 6.5.
Таблица 6.5. Грань Нормаль N6 N7 N8 N9 q6 N6 1 0,83 0,23 0,56 q7 N7 0,83 1 0 0 q8 N8 0,23 0 1 0 q9 N9 0,56 0 0 1 В результате анализа первой строки, соответствующей грани q6, находим грани {q6, q7, q9}, возможно, образующие некоторую вершину. В результате решения выделенной системы уравнений получаем точку (0, 55, 0). Эта точка не удовлетворяет ограничениям q4 >= 0 и q5 >= 0. Мы видим по рисунку 6.3, что ошибки бы не произошло, если бы из рассмотрения не была исключена грань q4. Мы делаем вывод о том, что "на стыке" поверхностей, где частично отсутствует информация об образующих некоторых вершин многогранника R, возможны ошибки. Нормаль к q4 составила бы с нормалью к q6 меньший угол, который был бы включен в формируемую комбинацию трех углов.
В результате анализа строки, соответствующей грани q7 (игнорируя нули), находим только грани q6 и q7. Однако для нахождения третьей грани придется все же организовать перебор (именно перебор) нулей. Проверим комбинацию граней {q6, q7, q8}. Их совместное решение определяет точку (0, 75, 0), не удовлетворяющую тем же ограничениям. Комбинация {q6, q7, q9} уже рассматривалась.
Анализ следующей строки приводит к необходимости проверки комбинаций {q6, q7, q8} и {q6, q8, q9}. Первая комбинация уже исследовалась, а вторая приводит к получению точки (5, 0, 0), удовлетворяющей всем ограничениям (точка B на рис. 6.3).
Анализ последней строки приводит к необходимости проверки комбинаций {q6, q7, q9} и {q6, q8, q9}. Обе комбинации уже рассматривались: первая — как неудачная, вторая — повторно образующая вершину.
-
Легко видеть, что если бы мы не выполняли перебор комбинаций нулей, то так и не получили бы вершину, так как при первой возможной комбинации, обусловленной алгоритмом, она ни разу не обнаружилась.
Отсюда вывод: в общем случае необходимо избегать анализа строк
матрицы S, соответствующих координатным плоскостям. Помимо того,
что
это — лишь возможные, но не действительные грани, углы, образуемые
нормалями к ним и нормалями к другим граням, могут превышать 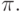 Это
с большой вероятностью приводит к ошибкам в определении соотношения
углов.
Это
с большой вероятностью приводит к ошибкам в определении соотношения
углов.
Так, в рассмотренном примере анализа верхней поверхности многогранника R достаточно было исследовать первые пять строк матрицы S ( табл. 6.1), опираясь на предположение о наличии "срединных" граней. Ведь в результате этого анализа вершины были найдены.
Напомним, что, выделяя верхнюю и нижнюю поверхности, мы некоторые вершины делаем недоступными для предлагаемого метода. Это — вершины "на стыке" поверхностей. В данном случае это, например, вершины, образуемые комбинациями {q1, q6, q8}, {q4, q6, q9} и др.
Рассмотренный пример анализа нижней поверхности многогранника R приводит к уточнению алгоритма нахождения опорного плана.
Нули — косинусы углов между осями координат — не всегда удается игнорировать. Это характерно для того случая, когда действительных граней, образующих рассматриваемую поверхность, недостаточно (r < n) или анализ соответствующих им строк матрицы S не приводит к успеху. Тогда приходится анализировать строки, соответствующие координатным плоскостям, "добирая" нулевые значения косинусов до общего количества n таких косинусов. При этом неизбежен перебор всех возможных комбинаций таких нулей.
Можно было бы сделать здесь вывод о том, что при подозрении о таких трудностях немедленно следует приступить к поиску опорного плана на другой поверхности. Однако мы не доказали, что хотя бы одна вершина обязательно будет найдена. Это приводит к необходимой готовности воспользоваться, в случае неудачи, одним из проверенных, традиционных методов нахождения опорного плана решения задачи ЛП, — более сложного и практически не распараллеливаемого.
Оценка сложности
Алгоритм поиска вершины многогранника допустимых решений предполагает ряд этапов.
-
Определение верхней (нижней) поверхности многогранника. Он заключается в проверке выполнения всех ограничений для точки начала координат. Сложность этого этапа можно оценить как O(nm). Число r граней-границ, образующих одну поверхность, не превышает m - 1,
r <= m - 1 (6.12)
-
Нахождение матрицы S косинусов углов между нормалями к действительным и возможным граням поверхности. Число таких косинусов для симметричной матрицы с учетом известных углов между осями координат составляет
Каждый косинус отыскивается в результате скалярного произведения единичных векторов нормалей, имеющего сложность O(6n). С учетом (6.12) можно оценить сложность алгоритма нахождения матрицы S как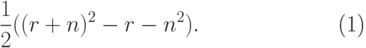
( 6.13) O(3m2n + mn2). (6.14)
-
Выделение n максимальных косинусов в каждой строке матрицы S. Сложность этой операции упорядочения по одной строке можно оценить как
O((m + n)2) (6.15)
-
Наконец, для выделенных граней необходимо решить систему n линейных уравнений, соответствующих этим граням. Сложность алгоритма такого решения составляет O(n3). Общая сложность выполнения этого этапа для всех строк составляет
O(mn3 + n4). (6.16)
Как видим, сложность нахождения вершины (точнее, всех возможных вершин) полиномиальная. Сумма степеней основных параметров n и m в составе членов полинома не превышает четырех.
В заключение отметим, что наметился общий прием распараллеливания решения задач оптимизации. Это не просто прием распараллеливания вычислений. Он определяет стратегию коллективного поведения компьютеров вычислительной системы или вычислительной сети при совместном решении задачи.
Алгоритм решения задачи предполагает, на разных этапах или глобально, варианты поиска промежуточных или окончательных решений. Компьютеры "расходятся" по отдельным вариантам поиска. Отдельный компьютер может достичь или не достичь успеха, реализуя стратегию "проб и ошибок". Тот компьютер, что достиг успеха, оперативно извещает другие компьютеры, которые прерывают свои действия. Все компьютеры используют успех одного для продолжения выполнения задачи.
Такой прием используется для поиска смежной вершины (по разным ребрам) с "лучшим" значением целевой функции при решении задачи ЛП. Такой же прием может применяться и для нахождения опорного плана решения этой же задачи. Ведь грани верхней (нижней) поверхности многогранника допустимых решений могут распределяться между компьютерами. Компьютер может для взятой на обработку грани найти все косинусы между ее нормалью и нормалями с другими гранями, и здесь не следует бояться повторения счета отдельных косинусов на разных компьютерах. Затем компьютер может выбрать n максимальных косинусов и проверить выделенную таким образом точку. Как только вершина найдена, работа других компьютеров по аналогичному поиску может быть прервана.
Однако возможно, и это должно быть исследовано статистически, что себя оправдает такая стратегия, когда в результате нахождения нескольких вершин в качестве опорного плана будет взято решение, обеспечивающее "лучшее" значение целевой функции.
Все сказанное наилучшим образом согласуется с SPMD-технологией "одна программа — много потоков данных ".
Вместе с тем, отметим, что здесь предлагается "инженерное" решение задачи на основе ее "физического смысла". Работа по обоснованию и строгому доказательству основных положений должна быть продолжена. Скорее всего, мы наблюдаем интересные свойства выпуклого многогранника допустимых решений задачи ЛП, не всегда умея их строго доказать.
