Диспетчирование параллельных вычислительных систем
Диспетчер последовательного назначения
Частичная упорядоченность работ отсутствует
Пусть на ВК или многопроцессорную ВС поступает поток заданий, которые объединяются в пакет. Каждое задание требует запуска соответствующей программы. Программы не зависят друг от друга, т.е. одни программы не используют результаты выполнения других в качестве исходных данных. Сформированный пакет заданий необходимо выполнить за минимальное время, добившись максимальной эффективности вычислительных средств. Это означает необходимость распределения работ по времени их выполнения "поровну" между процессорами ВС.
Данная задача известна как задача о рюкзаках и отображает необходимость распределения неделимых объектов (нельзя разрезать консервную банку или спальный мешок!) так, чтобы веса рюкзаков были как можно ближе к одинаковым.
Известен "хороший" эвристический алгоритм, для которого не удалось найти пример неточного оптимального распределения.
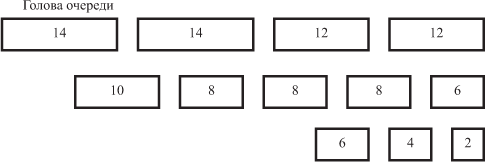
Формируется очередь заданий (программ), представляющая собой невозрастающую последовательность времен их выполнения. Например, такая очередь может иметь вид, представленный на рис. 10.1, где длина каждого прямоугольника условно соответствует времени выполнения программы, указанного внутри него.
Сформулируем основное правило назначения: исполнитель, набравший минимальный вес, берет работу из головы очереди.
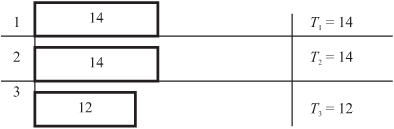
Пусть заданы три процессора-исполнителя. Первоначально все исполнители свободны. Тогда их приоритет обращения к очереди определяется их номерами. Очевидно, что при трехкратном обращении к очереди (каждым процессором) их загрузка будет выглядеть, как показано на рис. 10.2.
Справа на рисунке показана суммарная текущая загрузка каждого исполнителя.
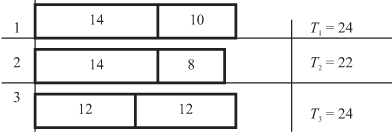
2. Так как теперь минимально загружен третий процессор, он выбирает работу с весом 12, и вся картина загрузки принимает вид, отраженный на рис. 10.3.
3. Затем последовательно назначаются на процессоры 1 и 2 работы с весами 10 и 8. Загрузка процессоров принимает вид, показанный на рис. 10.4.
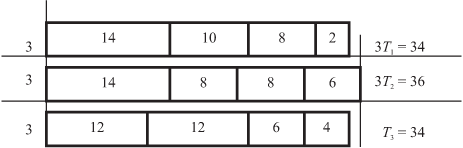
4. Продолжая таким же образом, получим окончательный план (рис. 10.5) выполнения работ.
Легко убедиться в том, что более "короткого" плана выполнения данного комплекса работ нет, т.е. распределение совпало с оптимальным.