Лекция 5: Параллельные методы расчета транспортной сети

Прямой перебор и аналог "симплекс-метода" при решении транспортной задачи без ограничения пропускной способности коммуникаций

Постановка задачи и планы решения

Пусть [15] в пунктах A₁, A₂, ... ,A_m производят некоторый однородный продукт в объеме a_i (i=1, 2, ... , m) единиц. В пунктах B₁, B₂, ... ,B_n этот продукт потребляется в объеме b_j ( j=1, 2, ... , n ) единиц. Из каждого пункта производства {A_i} возможна транспортировка в любой пункт потребления B_j. Транспортные издержки} по перевозке из пункта A_i в пункт B_j единицы продукции равны c_ij (i=1, ... , m; j=1, ... , n).

Необходимо найти такой план перевозок, при котором запросы всех потребителей полностью удовлетворены, весь продукт из пунктов производства вывезен и суммарные транспортные издержки минимальны.

Пусть x_ij — количество продукта, перевозимого из пункта A_i в пункт B_j. Требуется найти значение переменных (перевозок) x_ij >= 0 (i = 1, 2, ... , m ; j = 1, 2, ... , n), удовлетворяющих

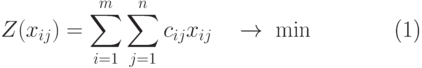( 5.1)

при ограничениях

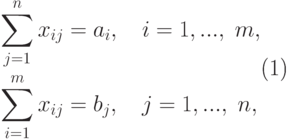( 5.2)

при условии неотрицательности

x_ij >= 0 (5.3)

и баланса

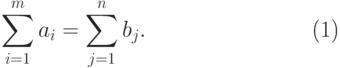( 5.4)

Сформулируем задачу линейного программирования в канонической постановке, исключив из (5.2) одно уравнение. При этом мы считаем, что условие баланса (5.4) оказывает влияние на корректность постановки задачи и учтено при этой постановке. Исключенное уравнение будем использовать также для контроля получаемого решения.

Следуя плану параллельного решения задачи линейного программирования и учитывая, что оптимальное решение находится хотя бы в одной из вершин многогранника допустимых решений, образуемого ограничениями и условиями, сформируем это множество граней. В его состав войдут m+n-1 выделенных уравнений-ограничений и m x n равенств нулю переменных на основе неотрицательности решения. Выбирая из этой системы по m x n уравнений с обязательным участием всех выделенных уравнений-ограничений и решая их совместно, мы можем находить вершины многогранника решений.

Так мы можем реализовать метод прямого перебора. Количество вариантов составляет C_{m x n}^{m x n - (m + n - 1)} . Это — количество различных способов приравнивания нулю m x n-(m+n-1) переменных из их общего числа m x n.

Мы можем реализовать и аналог симплекс-метода, найдя первоначально некоторую вершину, а затем перемещаясь по ребрам в одну из смежных вершин с большим значением целевой функции, пока это возможно.

Параллельный алгоритм решения

Исследование плана параллельного решения и формирование алгоритма будем сопровождать примером, для проверки правильности заимствованным в [15]. Для краткости условия (5.3) и (5.4) опущены.

Пример.

Z=7x₁₁+8x₁₂+5x₁₃+3x₁₄+2x₂₁+4x₂₂+5x₂₃+ +9x₂₄+6x₃₁+3x₃₂+1x₃₃+2x₃₄-> min (5.5)

при ограничениях

x₁₁ + x₁₂ + x₁₃ + x₁₄ = 11

x₂₁ + x₂₂ + x₂₃ + x₂₄ = 11

x₃₁ + x₃₂ + x₃₃ + x₃₄ = 8

x₁₁ + x₂₁ + x₃₁ = 5 (5.6)

x₁₂ + x₂₂ + x₃₂ = 9

x₁₃ + x₂₃ + x₃₃ = 9

x₁₄ + x₂₄ + x₃₄ = 7