Лекция 6: Некоторые задачи нелинейного программирования и нахождение опорного плана для задачи линейного программирования

Параллельное решение "плоской" задачи НП

Постановка задачи:

f(x,y)-> max

при ограничениях

g₁(x,y)>= 0

... g_m(x,y)>= 0

Могут быть условия x,y >= 0. Но они могут и отсутствовать, допуская поиск решения также в области отрицательных значений переменных.

Предположим:

1. Все ограничения разрешимы относительно всех переменных.
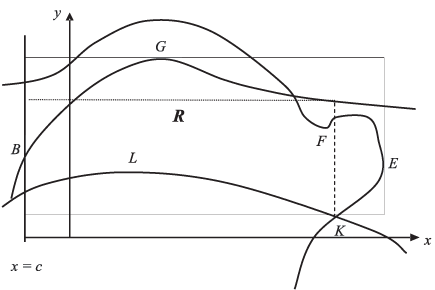
2. Ограничения и, возможно, условия неотрицательности решения образуют область R, ограниченную со всех сторон (рис. 6.2).

Рис. 6.2. "Плоская" нелинейная задача оптимизации с нелинейными ограничениями

Предположим, как на рисунке, m = 4. (Одно ограничение, x-c >=0, линейно.)

Решая попарно все равенства (границы R ), полученные по ограничениям, и проверяя точки пересечения на удовлетворение остальным неравенствам-ограничениям, найдём все вершины, в нашем примере — {A, B, C, K}.

Координаты найденных вершин дают начальную информацию (прямоугольник показан пунктиром) о "минимальном" прямоугольнике D, включающем в себя область R. Однако некоторые кривые, ограничивающие R, сопряженные с двумя вершинами, могут, имея экстремум по некоторым координатам между ними, "выходить" из этого прямоугольника. Точки такого выхода надо найти, проверить на принадлежность R, если они существуют, и расширить D.

Для каждого i = 1, ... , m, разрешим g_i относительно x. Получим (возможно, неоднозначную) функцию

.

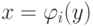Найдем множество экстремумов этой функции, решив уравнение

.

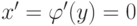Для каждой точки экстремума проверяем, принадлежит ли она области R, т.е. выполняются ли для нее все ограничения. Такой точкой на рисунке является точка E.

Теперь то же самое надо проделать, разрешив все функции g_i относительно y,

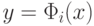
Найдем множество экстремумов этой функции, удовлетворяющих всем ограничениям. На рисунке это точки G, F, M, L.

Теперь мы нашли все точки, которые помогут нам очертить прямоугольник D, полностью вмещающий область R — область возможных решений задачи. Границы этого прямоугольника определяются минимальными и максимальными значениями координат всех найденных точек — точек пересечения кривых ограничений и точек экстремумов этих кривых, удовлетворяющих всем ограничениям задачи.

В нашем примере пусть A = (x_A, y_A), B = (x_B, y_B) и т.д. Тогда

x_D1 = min{x_A, x_B, x_G, x_C, x_F, x_E, x_M, x_K, x_L } = x_A = x_B,

x_D2 = max{x_A, x_B, x_G, x_C, x_F, x_E, x_M, x_K, x_L} = x_E,

y_D1 = min{y_A, y_B, y_G, y_C, y_F, y_M, y_E, y_K, y_L} = y_K,

y_D2 = max{y_A, y_B, y_G, y_C, y_F, y_M, y_E, y_K, y_L} = y_G.

Воспользуемся методом "сеток". Покроем область D сеткой с шагом 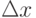по x и 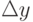по y. Испытывая каждый узел на принадлежность R, и находя в нем значение f(x, y), выберем максимальное.

Допускается обобщение метода решения для произвольной размерности.

Метод нормалей нахождения опорного плана для решения задачи линейного программирования

Предпосылки метода

Ниже предлагается метод нахождения вершины многогранника допустимых решений задачи линейного программирования для начала процесса параллельного поиска оптимального решения. В основе метода лежит предположение, что для некоторых вершин образующие их грани имеют нормали, которые составляют с каждой из этих нормалей минимальные углы. При обобщении на произвольное пространство обсуждается возможность использования косинусов углов между нормалями в качестве функции меры.

Параллельный алгоритм решения задачи линейного программирования (ЛП) ориентирован на применение SPMD-технологии ("одна программа — много потоков данных"), наиболее эффективной при организации распределенных (в локальной вычислительной сети) и параллельных (в многопроцессорной вычислительной системе) вычислений. Метод базируется на отказе от традиционного ввода свободных переменных. Поиск решения производится непосредственно в n -мерном пространстве, что сохраняет наглядность "физического смысла" задачи.

Суть метода в следующем. Первоначально должна быть известна некоторая вершина многогранника допустимых решений вместе с системой уравнений границ на основе ограничений и возможных границ — координатных плоскостей, которым эта вершина удовлетворяет. Эта вершина определяет начальный или опорный план. Далее с помощью множества процессоров вычислительной системы или рабочих станций вычислительной сети производится одновременное и независимое смещение вдоль ребер, исходящих из вершины, для поиска одной или более вершин с "лучшим" (большим или меньшим, в зависимости от поставленной задачи) значением целевой функции. Процессоры переключаются на новую вершину, и процесс продолжается до решения задачи.

Нетрадиционность этого подхода обусловлена высокой размерностью задачи и необходимостью распараллеливания. Распараллеливание требует, в свою очередь, пересмотра алгоритмов, ранее ориентированных только на сокращение количества операций и не обеспечивающих эффективную, одновременную загрузку оборудования, тем более — локальной вычислительной сети.

В лекции 4 курса "Архитектура параллельных вычислительных систем" даются рекомендации по параллельному нахождению опорного плана на основе прямого перебора. На задачах малой размерности, рассматриваемых в качестве примеров, это вполне допустимо, однако практическая задача размерности n = 36 и с числом ограничений m = 18 привела к недопустимому времени счета. Компьютеры стали бы искать опорный план не один месяц, что связано с экспоненциальной сложностью такого перебора.

Таким образом, необходимо найти "быстрый" параллельный алгоритм нахождения опорного плана.

Здесь можно было бы воспользоваться одним из известных "традиционных" методов. Однако желание максимально использовать "физический смысл" задачи и потому остаться в n -мерном пространстве сулит выявление замечательных свойств выпуклого многогранника допустимых решений, которые скрыты при традиционном абстрагировании.