Лекция 6: Некоторые задачи нелинейного программирования и нахождение опорного плана для задачи линейного программирования

Принцип внешней точки

Итак, поставлена задача ЛП

Z = c₁x₁ + c₂x₂ + ... + c_nx_n -> max

при ограничениях

q₁ = a₁₁x₁ + ... + a_1nx_n >= b₁ (6.1)

... q_m = a_m1x₁ + ... + a_mnx_n >= b_m

и при условии

x₁ >= 0, ... ,x_n >= 0.

Если в ограничениях заменить знак " " на "=", получим множество действительных (т.е. действительно являющихся) границ выпуклого многогранника R допустимых решений. Однако в общем случае часть его границ определяется условиями, также записанными в виде равенств. Это — возможные границы многогранника.

Таким образом, грани многогранника R формируются на основе множества m действительных и n возможных границ:

q₁ & = a₁₁x₁ + ... + a_1n x_n - b₁ = 0

...

q_m = a_m1x₁ + ... + a_mnx_n - b_m = 0 (6.2)

q_m+1 = x₁ = 0

...

q_m+n = x_n = 0.

Здесь обозначение q_i используется для названия соответствующих плоскостей и ограничений.

Тогда принципиально возможен выбор комбинаций по n уравнений из (6.2) и их совместное решение. Если решение существует, оно не отрицательно и удовлетворяет всем не использованным при этом ограничениям (6.1), то это решение определяет координаты одной из вершин многогранника R. Однако, как говорилось выше, нет гарантированных оценок времени получения первой вершины, а полный перебор Cⁿ_{m + n} систем n уравнений обладает экспоненциальной сложностью.

Локализуем поиск вершины многогранника R, освободившись от некоторых "лишних" уравнений из (6.2).

Установим направление роста целевой функции, записав ее дифференциал:

dZ = c₁dx₁ + c₂dx₂ + ... + c_ndx_n.

Сообщив одинаковое положительное приращение dx всем переменным, получим

dZ = (c₁ + c₂ + ... + c_n )dx.

Следовательно, сумма коэффициентов целевой функции (в отличие от более точной оценки с помощью градиента) определяет направление ее роста: если

( 6.3)

( 6.4)

Случай может быть причислен как к (6.3), так и к (6.4).

Выберем точку начала координат O (0, 0, ... , 0). Если все ограничения (6.1) в ней выполняются, эта точка является вершиной многогранника R, и наш поиск хотя бы одной вершины может быть успешно закончен. В противном случае будем считать эту точку внешней точкой, удобной для рассмотрения многогранника R "со стороны".

А именно, выделим множество тех плоскостей в (6.2), которые являются действительными гранями многогранника R и для которых в точке O выполняются ограничения задачи (6.1). Дополним это множество плоскостей n координатными плоскостями. Назовем образованную поверхность верхней поверхностью Q_верхн выпуклого многогранника R допустимых решений задачи ЛП. Координатные плоскости включаются в рассмотрение, для того чтобы можно было исследовать вершины R, принадлежащие этим плоскостям.

Аналогично, остальные плоскости (грани), для которых в точке O не выполняются ограничения (6.1), дополненные координатными плоскостями, образуют нижнюю поверхность Q_нижн многогранника R.

Очевидно, если сумма коэффициентов целевой функции положительна, то есть Z растет, удаляясь от точки O, то решение задачи ЛП следует искать среди вершин многогранника R на его верхней поверхности. В противном случае — на нижней поверхности.

Проследим на приведенном в лекции 4 курса "Архитектура параллельных вычислительных систем" примере рассматриваемые здесь построения. Для этого повторим постановку и дополним графическую интерпретацию представленной там задачи.

Задача формулировалась следующим образом:

Z = 26x + 20y + 21z -> max

при ограничениях

q₁ = 2x + 7y - 76z + 222 >= 0

q₂ = -8x + 9y - 8z + 64 >= 0

q₃ = -8x + 13y - 24z +96 >= 0 (6.5)

q₄ = -x - 6y - z + 70 >= 0

q₅ = -2x - 7y - 2z + 90 >= 0

q₆ = 33x + 3y + 22z - 165 >= 0

и при условии неотрицательности переменных, о чем в дальнейшем можно не упоминать.

Так как сумма коэффициентов целевой функции положительна, то нас будет интересовать верхняя поверхность многогранника R допустимых решений. При x = y = z = 0 справедливы неравенства для q₁ ,... , q₅. Следовательно,

Q_верхн = {q₁, q₂, q₃, q₄, q₅, q₇, q₈, q₉}. (6.6)

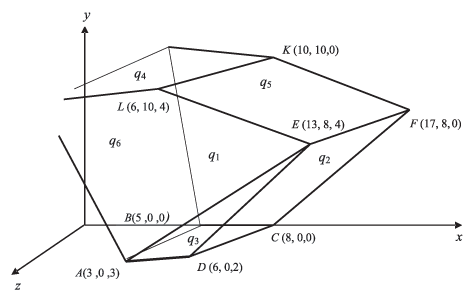
На рис. 6.3 3 ребра верхней поверхности выделены. Координаты точек выбраны при построении примера и приведены для контроля. Считаем их неизвестными; их необходимо получить.

Рис. 6.3. Многогранник допустимых решений с выделенными рёбрами

В данном случае мы получили малый выигрыш, исключив из рассмотрения единственную грань с образуемыми ею вершинами. Однако в произвольном случае форма R может быть разнообразной, и подобное сокращение рассматриваемых ограничений, то есть связанных с ними граней, может быть существенным. Да и сейчас мы видим, что число вершин, среди которых необходим поиск, весьма сократилось — до шести отмеченных на рисунке.