Лекция 6: Некоторые задачи нелинейного программирования и нахождение опорного плана для задачи линейного программирования
Основные предположения
Определение. Назовем плоскость в n -мерном пространстве образующей вершины A выпуклого многогранника R допустимых решений задачи ЛП, если ее уравнение входит в состав системы n линейных уравнений границ многогранника R, решением которой является точка A.
В общем случае каждая вершина многогранника R имеет не менее n образующих плоскостей. Часть из них может совпадать с координатными плоскостями.
Изменим обозначение плоскостей-граней, образующих исследуемую далее верхнюю (нижнюю) поверхность многогранника R:
Qверхн (Qнижн) ={p1, p2,... , pr, pr+1, ... ,pr+n}. (6.7)
Здесь  , j = 1, ... , r, —
действительные плоскости грани, pr+k = qm+k, k = 1, ... , n, —
координатные плоскости.
, j = 1, ... , r, —
действительные плоскости грани, pr+k = qm+k, k = 1, ... , n, —
координатные плоскости.
Сменим обозначение и коэффициентов уравнений плоскостей, выделив совокупность всех граней многогранника R — действительных и возможных, образующих исследуемую (верхнюю или нижнюю) поверхность:
p1 = d11 x1 + d12 x2 +... + d1n xn = 0
p2 = d21 x1 + d22 x2 +... + d2n xn = 0
...
pr = dr1 x1 + dr2 x2 +... + dr n xn = 0 (6.8)
pr+1 = x1 = 0
...
pr+n = xn = 0.
Найдем координаты единичных векторов нормалей Nj, j = 1,... , n+r, к плоскостям (6.8):
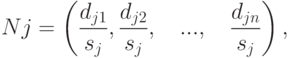 |
( 6.9) |
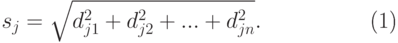 |
( 6.10) |
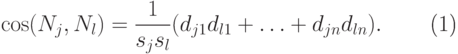 |
( 6.11) |
Если плоскости pj и pq совместно не являются
образующими
какой-либо вершины верхней (нижней) поверхности выпуклого
многогранника R допустимых решений задачи ЛП, а их нормали Nj и Nq образуют "угол" 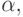 то
существует плоскость pl с
нормалью Nl, совместно с pj являющаяся образующей
некоторой
вершины этой же поверхности и такая, что "угол"
то
существует плоскость pl с
нормалью Nl, совместно с pj являющаяся образующей
некоторой
вершины этой же поверхности и такая, что "угол"  между
нормалями Nj и Nl меньше угла
между
нормалями Nj и Nl меньше угла 
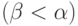 ).
).
Слово "угол" берем в кавычки в связи с тем, что любой угол измеряется в плоскости и видеть его мы можем в двух- и трехмерном пространстве.
В общем случае n -мерного пространства мы можем судить о величине угла по его косинусу, который отыскивается как результат скалярного произведения единичных векторов. Отсюда следует, что геометрически мы можем продемонстрировать верность гипотезы в двух- и трехмерном пространстве. В общем же случае доказательство ее справедливости должно быть аналитическим.
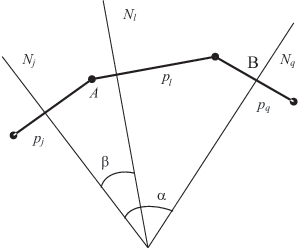
Итак, поясним высказанное предположение "плоским" рис. 6.4.
Выделим произвольную вершину A многогранника R.
Она
"окружена" образующими ее гранями (на плоскости — ребрами). Пусть pj — одна из них. Любая грань, не являющаяся образующей
вершины A,
например — грань (ребро) pq, добавляет угол излома поверхности
в угол
наклона  ее нормали Nq. Точка пересечения pj и pq находится
вне R. Тогда должна существовать образующая эту же вершину грань
(ребро) pl, нормаль к которой Nl имеет меньший
угол наклона,
ее нормали Nq. Точка пересечения pj и pq находится
вне R. Тогда должна существовать образующая эту же вершину грань
(ребро) pl, нормаль к которой Nl имеет меньший
угол наклона, 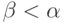 .
.
Представим (рис. 6.5) аналогичную картину в трехмерном пространстве.
Пусть p2 и p3 не являются смежными на данной
поверхности
многогранника R, то есть не имеют общего ребра и, следовательно,
совместно не являются образующими какой-либо вершины. Тогда
существует одна или более разделяющих их граней, здесь, например — грань p1, нормаль к которой N1 образует с нормалью N2 угол  меньший угла
меньший угла  — угла между нормалями N2 и N3.
— угла между нормалями N2 и N3.
Минуя формальное и строгое доказательство, продолжим пояснение гипотезы на качественном уровне.
Грани p1 и p2 являются образующими двух вершин A и B. Для гарантии смежности этих граней, то есть того, что они совместно являются образующими какой-то вершины, можно в основу выбора такой вершины положить минимальный угол между нормалями к ним. То есть будем считать, что если для фиксированной грани pj найден минимальный из углов между нормалью Nj к этой грани и нормалями ко всем другим граням этой же поверхности, — угол между нормалью Nj и нормалью Nl, то две грани pj и pl совместно являются образующими хотя бы одной вершины этой поверхности.
Чтобы найти третью грань — третье уравнение для нахождения точки в трехмерном пространстве, следует искать такую грань (например, p4 на рис. 6.5), между нормалью к которой и нормалями N1 и N2 углы также меньше тех углов, которые N1 и N2 образуют с нормалями несмежных граней. Такая грань будет смежной и p1, и p2.
Теорема. Пусть p — произвольная грань верхней (нижней) поверхности многогранника R допустимых решений задачи ЛП. Составим неубывающую последовательность углов между нормалью к этой грани и нормалями всех граней этой же поверхности (включая нормаль к этой же грани; этот угол равен нулю). Первые n минимальных отличных от нуля углов этой последовательности указывают на n граней, являющихся образующими некоторой вершины многогранника R.
Доказательство. Пусть среди выделенных таким образом граней есть грань, не являющаяся совместно с другими образующей одной вершины. Тогда, по теореме-гипотезе, существует образующая ту же вершину грань, не параллельная первой и такая, нормаль к которой составляет с нормалью к p угол, меньший, чем выделенный по указанной последовательности. Это противоречит правилу выбора n минимальных углов.