|
Упражнение 2.1.25 |
Конечные автоматы
2.6. Детерминированные конечные автоматы
Определение 2.6.1.
Конечный автомат  называется детерминированным
(deterministic),
если
называется детерминированным
(deterministic),
если
- множество I содержит ровно один элемент;
- для каждого перехода
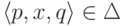 выполняется равенство |x| = 1 ;
выполняется равенство |x| = 1 ; - для любого символа
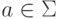 и для любого состояния
и для любого состояния  существует не более одного состояния
существует не более одного состояния 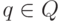 со свойством
со свойством 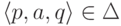 .
.
Пример 2.6.2. Конечный автомат из примера 2.1.14 является детерминированным.
Определение 2.6.3.
Детерминированный конечный автомат 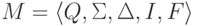 называется полным (complete),
если для каждого состояния
называется полным (complete),
если для каждого состояния  и для каждого символа
и для каждого символа 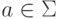 найдется такое состояние
найдется такое состояние 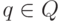 ,
что
,
что 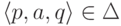 .
.
Пример 2.6.4.
Конечный автомат из примера 2.1.14
эквивалентен полному детерминированному конечному автомату  ,
где Q = {1,2,3},
,
где Q = {1,2,3},  , I = {1}, F = {1,2},
, I = {1}, F = {1,2},
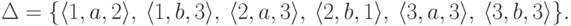
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" <0.6mm> ^{a}
\ar "2,2" _{b}
& *=[o][F=]{2}
\ar "1,1" <0.6mm> ^{b}
\ar "2,2" ^{a}
\\
%
& *=[o][F-]{3}
\rloop{1,0} ^{a}
\rloop{0,-1} ^{b}
}](/sites/default/files/tex_cache/137f2b115f8d217ee9866f93436cd22a.png)
Замечание 2.6.5.
Некоторые авторы используют в определении
полного детерминированного конечного автомата вместо
отношения  функцию
функцию 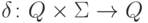 .
От функции
.
От функции  можно перейти
к отношению
можно перейти
к отношению  ,
положив
,
положив
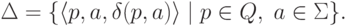
Упражнение 2.6.6. Является ли детерминированным следующий конечный автомат?
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix @=1mm{
%
&
& *=[o][F-]{2}
\ar "2,5" ^{b}
\rloop{0,1} ^{a}
\rloop{0,-1} _{b}
&
&
\\
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "1,3" ^{a}
\ar "3,3" ^{b}
&
&
&
& *=[o][F=]{4}
\\
%
&
& *=[o][F-]{3}
\rloop{0,1} _{a}
\rloop{0,-1} ^{b}
\ar "2,5" ^{a}
&
&
}](/sites/default/files/tex_cache/6729c3af8584fabc3cb10f66e74b6029.png)
Упражнение 2.6.7. Является ли полным следующий
детерминированный конечный автомат с алфавитом 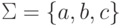 ?
?
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a}
\rloop{0,-1} ^{b}
\ar "1,2" ^{c}
& *=[o][F-]{2}
\rloop{0,1} ^{a}
\rloop{0,-1} ^{b}
\ar "1,3" ^{c}
& *=[o][F=]{3}
\rloop{0,1} ^{a}
\rloop{0,-1} ^{b}
\rloop{1,0} ^{c}
}](/sites/default/files/tex_cache/5b302650f6bcfbefe68383da9bb69af6.png)
2.7. Преобразование конечного автомата к детерминированному виду
Теорема 2.7.1 Каждый автоматный язык распознается некоторым полным детерминированным конечным автоматом.
Доказательство.
Без ограничения общности можно предположить,
что исходный язык задан конечным автоматом  ,
содержащим только переходы с метками длины единица.
Для любых
,
содержащим только переходы с метками длины единица.
Для любых 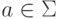 и
и 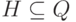 обозначим
обозначим

Обозначим через 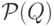 множество всех подмножеств множества Q.
Построим искомый полный детерминированный конечный автомат
множество всех подмножеств множества Q.
Построим искомый полный детерминированный конечный автомат 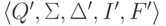 ,
положив
,
положив 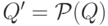 ,
,
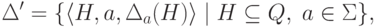
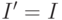 и
и  .
.Пример 2.7.2.
Пусть  .
Рассмотрим конечный автомат
.
Рассмотрим конечный автомат 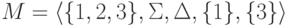 ,
где
,
где
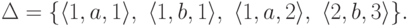
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{a}
\rloop{0,-1} ^{b}
\ar "1,2" ^{a}
& *=[o][F-]{2}
\ar "1,3" ^{b}
& *=[o][F=]{3}
}](/sites/default/files/tex_cache/a9d5e9fb82e39214b8627cc613b269c8.png)
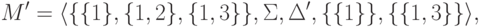
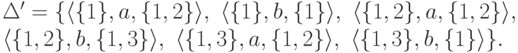
![\objectwidth={7.5mm} \objectheight={7.5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{b}
\ar "1,2" ^{a}
& *=[o][F-]{1,2}
\rloop{0,1} ^{a}
\ar "2,2" <0.6mm> ^{b}
\\
%
& *=[o][F=]{1,3}
\ar "1,2" <0.6mm> ^{a}
\ar "1,1" ^{b}
}](/sites/default/files/tex_cache/287a3c7a2a42a4e1524d18ea1f71253c.png)
Упражнение 2.7.3. Найти полный детерминированный конечный автомат, эквивалентный автомату, изображенному на диаграмме.
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "2,1" ^{ab}
\\
*=[o][F=]{2}
\ar @`{+/l16mm/} [] ^{}
\rloop{1,0} ^{a}
}](/sites/default/files/tex_cache/9e4e2ff692126aae7c7f277b2953a246.png)
Упражнение 2.7.4. Найти детерминированный конечный автомат для языка, порождаемого грамматикой

Упражнение 2.7.5. Найти детерминированный конечный автомат, распознающий
язык 
