|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Лекция 4: Отслеживание движения и алгоритмы сопровождения ключевых точек
2.7. Применение фильтра частиц к задаче сопровождения
Для некоторых практических задач, чтобы получить более точную оценку состояния системы, необходимо уйти от предположения, что шум имеет Гауссово распределение [5]. В этом случае вводится понятие мультимодального распределения7Мультимодальным распределением называется распределение, имеющее несколько мод или локальных максимумов. Мультимодальное распределение зачастую представляется смесью нескольких распределений. шума, а для моделирования подобных систем используются фильтры частиц. Фильтры частиц являются более общим подходом к решению задачи сопровождения с применением вероятностных методов [9, 21, 33, 35].
Алгоритм воспроизведения условной плотности (CONditional DENSity propAGATION, CONDENSATION) [21, 35] – базовый алгоритм фильтрации частиц, на основании которого строится большинство алгоритмов данной группы, применяемых в компьютерном зрении. Поэтому остановимся более детально на рассмотрении схемы работы именно этого алгоритма.
Предполагая, что система может находиться в состояниях
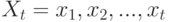 , в момент времени получим плотность распределения
вероятности. Так же, как и для фильтра Кальмана, последовательность
наблюдений будем обозначать
, в момент времени получим плотность распределения
вероятности. Так же, как и для фильтра Кальмана, последовательность
наблюдений будем обозначать 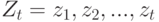 . Наряду с этим введем
предположение о том, что состояние
. Наряду с этим введем
предположение о том, что состояние 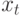 зависит только от предыдущего
состояния
зависит только от предыдущего
состояния 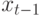 – условие Марковской цепи. Таким образом, получаем
систему с независимым набором наблюдений. Техники фильтрации частиц
представляют распределение вероятности в виде коллекции взвешенных
выборок – частиц, появление которых регулируется посредством введения
весов. Тогда множество
– условие Марковской цепи. Таким образом, получаем
систему с независимым набором наблюдений. Техники фильтрации частиц
представляют распределение вероятности в виде коллекции взвешенных
выборок – частиц, появление которых регулируется посредством введения
весов. Тогда множество 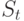 (4.60) определяет функцию плотности
вероятности для состояния
(4.60) определяет функцию плотности
вероятности для состояния 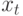 при заданном наборе наблюдений
при заданном наборе наблюдений 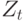 .
.
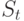 задает приближенное распределение
задает приближенное распределение  .
.
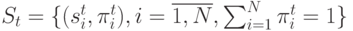 |
( 4.60) |
Задача состоит в том, чтобы построить метод восстановления множества  на основании
на основании 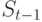 . Формально алгоритм можно представить в виде
последовательности этапов [9, 21, 35]:
. Формально алгоритм можно представить в виде
последовательности этапов [9, 21, 35]:
- Пусть коллекция взвешенных выборок в момент времени
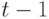 построена (4.61).
Дополнительно вычислим интегральные веса согласно (4.62).
построена (4.61).
Дополнительно вычислим интегральные веса согласно (4.62).
( 4.61) 
( 4.62) - Определим n-ый экземпляр выборки
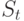 . Для этого случайным образом
выберем число r из отрезка [0,1] и вычислим
. Для этого случайным образом
выберем число r из отрезка [0,1] и вычислим  .
Отсюда получаем текущую оценку состояния
.
Отсюда получаем текущую оценку состояния  .
. - Выполним предсказание следующего состояния. Предсказание (4.63)
выполняется аналогично фильтру Кальмана (4.40), разница лишь в том,
что нет ограничений, связанных с линейностью системы и видом
распределения шума.

( 4.63) - Выполним коррекцию. Используя текущее наблюдение и его
распределение, необходимо установить вес полученного экземпляра
согласно (4.64).

( 4.64) - Построим множество частиц , повторив шаги 2 – 4 -раз.
- Нормализуем последовательность весов
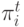 так, чтобы
так, чтобы  .
. - Вычислим наилучшую оценку для состояния
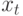 , например, как
линейную свертку полученного набора экземпляров выборки (4.65).
Таким образом, фактически определим некоторую среднюю частицу.
, например, как
линейную свертку полученного набора экземпляров выборки (4.65).
Таким образом, фактически определим некоторую среднюю частицу.

( 4.65)
Описанный процесс можно проинтерпретировать графически (рис.4.8) с
использованием понятия частицы. На входе итерации алгоритма имеется
множество частиц  (верхний уровень диаграммы). В
результате N-кратного случайного выбора частиц из
(верхний уровень диаграммы). В
результате N-кратного случайного выбора частиц из 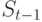 получается
некоторый набор экземпляров (2-ой уровень сверху). Применение шага
предсказания приводит к формированию множества оценочных состояний
частиц (3-ий уровень), затем для каждой оценки выполняется коррекция на
основании имеющихся наблюдений. Как следствие, создается множество
частиц
получается
некоторый набор экземпляров (2-ой уровень сверху). Применение шага
предсказания приводит к формированию множества оценочных состояний
частиц (3-ий уровень), затем для каждой оценки выполняется коррекция на
основании имеющихся наблюдений. Как следствие, создается множество
частиц  в следующий момент времени (последний уровень
диаграммы).
в следующий момент времени (последний уровень
диаграммы).
3. Контрольные вопросы
- В каких случаях схема вычитания фона в задаче определения движения работает неэффективно?
- Докажите, что формула (4.25) справедлива, т.е. образ Фурье от корреляции пары функций равен произведению образу Фурье первой функции на комплексно-сопряженный образ второй функции.
- Основное свойство аффинного преобразования?
- Приведите примеры задач, в которых используется модель перспективной проекции (гомография).
- Докажите справедливость формул (4.58) и (4.59).
- Получите формулы вычисления матричного коэффициента Кальмана для случая равномерного движения.
- Приведите схему построения фильтра Кальмана в случае одномерного
состояния и наблюдения при некоторых фиксированных значениях
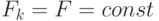 и
и 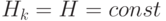 .
.


![Итерация алгоритма воспроизведения условной плотности (CONDENSATION, [35])](/EDI/16_08_14_2/1408137470-25747/tutorial/1179/objects/4/files/04_08.jpg)
 "
"