|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Лекция 4: Отслеживание движения и алгоритмы сопровождения ключевых точек
На основании такого правила формируется двумерная маска.
Чтобы обработать следующий кадр, необходимо обновить
параметры распределений: математическое ожидание
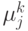 и
среднеквадратичное отклонение
и
среднеквадратичное отклонение 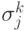 . В зависимости от того,
нашлось ли соответствующее распределение для цвета текущего
пикселя, обновление выполняется по-разному.
. В зависимости от того,
нашлось ли соответствующее распределение для цвета текущего
пикселя, обновление выполняется по-разному.
- Соответствие обнаружено. Тогда весовые коэффициенты,
составляющие смесь Гауссовых распределений, которым
соответствует
 и параметры распределений
пересчитываются согласно формулам (4.14) – (4.16).
и параметры распределений
пересчитываются согласно формулам (4.14) – (4.16).
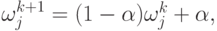
( 4.14) 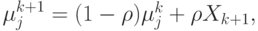
( 4.15) где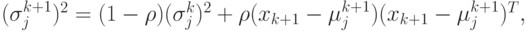
( 4.16)  – заданная константа,
– заданная константа, 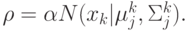 .
Для всех распределений, которым
.
Для всех распределений, которым  не соответствует,
параметры не изменяются, только пересчитываются
коэффициенты
не соответствует,
параметры не изменяются, только пересчитываются
коэффициенты 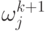 согласно (4.17).
согласно (4.17).
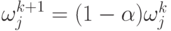
( 4.17) - Соответствие не найдено. В данном случае крайнее (в смысле
введенного отношения порядка) распределение Гаусса
замещается распределением с новыми параметрами.
Математическое ожидание выбирается равным текущему
значению цвета пикселя
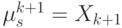 дисперсия
дисперсия 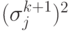 максимально возможной, а вес
максимально возможной, а вес 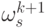 минимально допустимым.
минимально допустимым.
В завершении отметим, что количество распределений определяется сложностью фона и имеющимися вычислительными мощностями (в [2] предлагается использовать значение в пределах от 3 до 5). Начальная инициализация параметров распределений может выполняться с использованием метода k-средних [2], либо EM-алгоритма (Expectation Maximization) [4, 32].
На рис.4.1 показан пример применения метода вычитания фона с представлением модели фона смесью Гауссовых распределений.

Рис. 4.1. Пример применения метода вычитания фона с использованием метода представления фона смесью Гауссовых распределений
Метод представления модели фона смесью Гауссовых распределений2Результат получен с помощью реализации BackgroundSubtractorMOG2 библиотеки OpenCV. обладает рядом недостатков. Во-первых, метод не приспособлен к резким изменениям освещения, что является естественным для некоторых видео. Во-вторых, начальная инициализация параметров распределений является достаточно трудоемкой процедурой. Относительно большое количество параметров требует организации подбора наиболее оптимальных значений для конкретных данных.
Метод извлечения визуального фона (Visual Background
Extractor , ViBe) [12]. В соответствии с данным методом модель
фона на кадре с номером 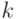 представляется набором множеств
представляется набором множеств
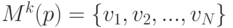 для всех пикселей
для всех пикселей 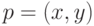 где
где 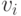 –
интенсивность/цвет пикселя (в общем случае вектор).
–
интенсивность/цвет пикселя (в общем случае вектор).
Для классификации пикселя в цветовом пространстве строится
сфера 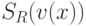 радиуса R и определяется количество векторов
множества
радиуса R и определяется количество векторов
множества
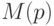 которые попадают вовнутрь построенной сферы,
которые попадают вовнутрь построенной сферы,
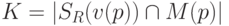 . Если
. Если 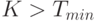 , где
, где  – фиксированное пороговое значение, то принимается, что пиксель принадлежит
фону, в противном случае, объекту.
– фиксированное пороговое значение, то принимается, что пиксель принадлежит
фону, в противном случае, объекту.
На начальном этапе необходимо выполнить инициализацию
множеств 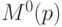 для всех пикселей следующим образом:
для всех пикселей следующим образом:
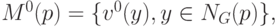 |
( 4.18) |
где 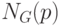 – окрестность пикселя размера 3x3 (9 клеток, включая
текущий пиксель), y выбирается
– окрестность пикселя размера 3x3 (9 клеток, включая
текущий пиксель), y выбирается  раз случайным образом.
Обновление модели фона для кадра
раз случайным образом.
Обновление модели фона для кадра  выполняется в два шага:
выполняется в два шага:
- Если p проклассифицирован как пиксель фона, то из множества
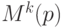 случайно выбирается компонента, которая заменяется
значением
случайно выбирается компонента, которая заменяется
значением 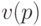 .
. - Случайным образом выбирается один соседний пиксель из
окрестности
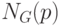 , для которого выполняется предыдущий
шаг.
, для которого выполняется предыдущий
шаг.
Множество методов построения моделей фона не ограничивается набором методов, представленных в этом разделе. В данном направлении ведутся активные исследования до настоящего момента. Поэтому здесь представлены лишь принципиально разные подходы к решению задачи построения фоновых моделей.

 "
"