Лекция 4: Отслеживание движения и алгоритмы сопровождения ключевых точек

1.2. Вычитание фона

Наиболее простой подход к решению данной задачи состоит в том, чтобы использовать механизм вычитания фона из кадра видео (background subtraction) [6 – 9]. Процедура вычитания предполагает, что для данного видео построена модель фона (4.3):

( 4.3)

также возможно существует механизм обновления модели фона с течением времени. Для одноканального (в оттенках серого) изображения, т.е. когда 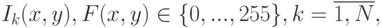процедуру вычитания можно разбить на два этапа:

1. Вычитание фонового изображения из текущего кадра видео. Данный шаг включает в себя попиксельное вычитание интенсивностей кадра видео и фонового изображения (4.4).

   ( 4.4)

2. Отбор пикселей, принадлежащих фону и объекту, – построение бинарного изображения (маски). Считается, что пиксель принадлежит объекту и имеет белый цвет в маске, если разность интенсивности фона и текущего кадра для данного пикселя превышает некоторое пороговое значение в противном случае, принимается, что пиксель принадлежит фону (4.5).

   ( 4.5)

Дополнительно к указанным операциям с целью повышения качества поиска может выполняться, например, фильтрация кадров исходного потока видеоданных, либо фильтрация бинарного видео, также могут применяться морфологические операции к полученному отсечению с целью удаления шумов [8]. Если имеется цветное изображение, то его всегда можно преобразовать в оттенки серого.

Качество определения положения движущихся областей посредством вычитания фона во многом зависит от качества построенной модели фона. Множество всех техник вычитания фона подразделяется на две группы в зависимости от механизма построения фонового изображения:

1. Нерекурсивные. Нерекурсивные методы обновляют модель фона для текущего кадра на основании информации об интенсивностях пикселей некоторого набора предшествующих моделей фона [6] (или кадров) и текущего кадра. К наиболее распространенным нерекурсивным методам относятся следующие методы:

• Метод вычитания текущего и предыдущего кадра . Согласно данному методу считается, что для кадра модель фона совпадает с предыдущим кадром, т.е. . Тогда на первом этапе алгоритма вычитания фона вычисляется разница пары последовательно идущих кадров (4.6).

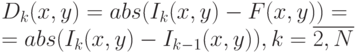
  ( 4.6)

• Метод усреднения определенного количества предшествующих кадров . Обозначим количество кадров, по которым будет выполняться построение модели фона, как s. Тогда для кадра модель фона определяется в соответствии с формулой (4.7).

  ( 4.7)

• Метод определения медианы фиксированного количества предшествующих кадров . Пусть s – число кадров, на основании которых будет обновляться модель фона. Тогда модель фона вычисляется согласно формуле (4.8).

  ( 4.8)

Основное преимущество нерекурсивных методов – простота реализации и скорость обновления моделей фона при переходе от кадра к кадру. При этом заметим, что качество работы методов данной группы в значительной степени зависит от скорости объектов. Медленно перемещающиеся объекты, как правило, обнаруживаются плохо. Более того, приведенные методы не дают качественный результат при изменении света на сцене, либо при наличии динамического фона (листва деревьев, струящаяся вода и т.п.). Чтобы сгладить влияние указанных эффектов, обновленная модель фона для кадра представляется выпуклой оболочкой модели фона 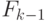с текущим изображением (4.9). Такая процедура называется -смешиванием.

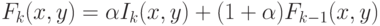( 4.9)

2. Рекурсивные. Рекурсивные методы для обновления модели фона используют информацию об интенсивностях пикселей только текущего кадра. К методам данной группы относятся гистограммный метод, метод представления модели фона смесью Гауссовых распределений (Gaussian mixture model) [2, 3, 9], метод "шифровальной" книги (codebook) [10, 11], метод извлечения визуального фона (Visual Background Extractor, ViBe) [12]. Рассмотрим некоторые из перечисленных методов.

• Гистограммный метод. Идея гистограммного метода состоит в том, что все цветовое пространство разбивается на отдельные бины (для полутонового изображения пространство представляет отрезок изменения интенсивности, в случае цветного изображения – трехмерный куб). Для каждого изображения в последовательности выполняется построение гистограммы. Осуществляется проход по всем пикселям изображения, в зависимости от того, какая интенсивность/цвет наблюдается в пикселе, увеличивается на единицу величина соответствующего бина гистограммы. Принимается, что пиксели, составляющие некоторый бин, принадлежат фону, если величина данного бина меньше фиксированного порогового значения, в противном случае, считается, что они принадлежат объекту. Основная проблема применения гистограммного метода состоит в необходимости использования дополнительной памяти, а также в выполнении большого количества операций обращения к памяти в процессе реализации.
• Смесь Гауссовых распределений. При построении фона с использованием данного метода считается, что для любого пикселя 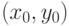изображения известна история изменения его интенсивности/цвета на всех предшествующих кадрах . Тогда вероятность того, что наблюдается значение , может быть представлена смесью из Гауссовых распределений (4.10).

( 4.10)

где 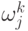– вес j-ого распределения Гаусса для кадра с номером , – математическое ожидание, – среднеквадратичное отклонение, – функция плотности нормального распределения (4.11).

( 4.11)

Предполагается, что компоненты цвета независимы и имеют одинаковое среднеквадратичное отклонение. Поэтому матрица ковариации имеет вид , где E – единичная матрица.

Указанное предположение позволяет снизить вычислительную трудоемкость метода за счет отсутствия необходимости вычислять матрицу, обратную к матрице ковариации 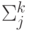в (4.11). Таким образом, задано распределение наблюдаемых значений цвета для каждого пикселя. Новое значение будет представляться одной из основных компонент построенной смеси Гауссовых распределений и использоваться для обновления параметров модели. Распределения сортируются в порядке уменьшения величины . Такая сортировка предполагает, что пиксель фона отвечает распределению с большим весом и малой дисперсией.

Принимается, что первые распределений, удовлетворяющих условию (4.12), соответствуют распределению цвета фоновых пикселей.

( 4.12)

где T – некоторое пороговое значение, параметр модели. Когда приходит очередной кадр , для каждого пикселя изображения выполняется тест, который позволяет определить с использованием расстояния Махаланобиса, какому распределению соответствует полученное значение (4.13).

( 4.13)

1. Если нашлось соответствующее распределение Гаусса, то в зависимости от того, определяет ли оно распределение фоновых пикселей (входит в группу из распределений) или нет, текущий пиксель классифицируется как фоновый, либо как принадлежащий объекту.
2. Если не обнаружилось ни одного распределения, удовлетворяющего условию (4.13), то считается, что пиксель принадлежит объекту.