|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Лекция 4: Отслеживание движения и алгоритмы сопровождения ключевых точек
1.4. Параметрические модели движения
Многие прикладные задачи, такие, как склеивание изображений в
панораму, стабилизация видео, требуют построения более сложных
моделей движения, т.к. движение не описывается только линейным
сдвигом. Поэтому рассматриваются пространственные поля смещений, и
выполняется построение параметрических моделей движения
(parametric motion, [5, гл. 8.2]). В параметрических моделях вместо
постоянного вектора смещения![[u,v]^T](/sites/default/files/tex_cache/8f2c7a5a1502a634df4a3a3500db7001.png) рассматривается параметризованное
поле смещений
рассматривается параметризованное
поле смещений
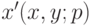 , где p-вектор параметров. Приведем некоторые
примеры параметризованных моделей:
, где p-вектор параметров. Приведем некоторые
примеры параметризованных моделей:
- Линейный сдвиг (4.29).
где

( 4.29) 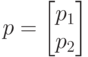 – вектор сдвига.
– вектор сдвига. -
Поворот со сдвигом (4.30).
где

( 4.30) 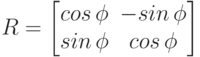 – ортонормированная матрица поворота, т.е.
– ортонормированная матрица поворота, т.е.
 и
и 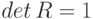 ,
, 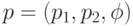 – набор параметров модели
движения.
– набор параметров модели
движения. -
Преобразование подобия (4.31).
где
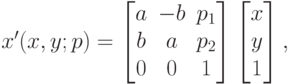
( 4.31)  – матрица поворота, умноженная на коэффициент
масштабирования
– матрица поворота, умноженная на коэффициент
масштабирования  – набор параметров модели
движения.
– набор параметров модели
движения. -
Аффинное преобразование (4.32).
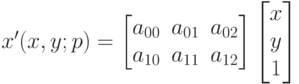
( 4.32) -
Перспективная проекция или гомография (4.33).

( 4.33)
Аналогично процедуре уточнения направления, описанной в разделе 1.3, можно выполнить определение направления движения для любой параметрической модели (4.35), расписав квадратичную функцию ошибки (4.34) с помощью разложения в ряд Тейлора по вектору параметров и выполнив ее минимизацию.

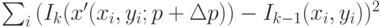 |
( 4.34) |
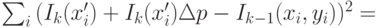
 |
( 4.35) |
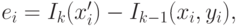
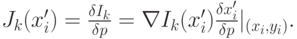
1.5. Многоуровневое движение
Во многих случаях визуальное движение вызвано смещением небольшого количества объектов, находящихся на разной глубине изображения [5]. Поэтому движение пикселей можно описать более эффективно, если сгруппировать их в слои [14], и отслеживать многоуровневое движение (layered motion, [5, гл. 8.5]) построенных слоев, например, с помощью параметрических моделей [15].
Последовательно рассмотрим основные вопросы, которые возникают в процессе определения многоуровневого движения, и схемы их решения, предложенные в одной из первых работ по данной тематике [15].
1. Как представить слой? Слой определяется набором из трех карт (матриц):
- матрица интенсивности слоя (в компьютерной графике текстурная карта);
-
 карта, которая определяет прозрачность слоя в каждом точке
изображения;
карта, которая определяет прозрачность слоя в каждом точке
изображения; - карта скоростей описывает изменение положения точек с течением времени.
Ниже (рис.4.3) показан пример представления кадров в виде набора слоев. Изображения в строке (а) соответствуют фоновому слою, в строке (b) – слою, содержащему объект (рука), в (с) – последовательность изображений, восстановленная на основании выделенных слоев.
Предположим, что 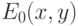 – матрица интенсивности фонового слоя,
– матрица интенсивности фонового слоя,
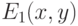 – слоя, содержащего объект,
– слоя, содержащего объект,  –
–  -карта слоя
-карта слоя 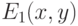 .
Поскольку слои перекрываются, то для представленного примера
восстановить можно исходное изображение согласно (4.36).
.
Поскольку слои перекрываются, то для представленного примера
восстановить можно исходное изображение согласно (4.36).
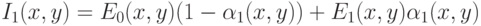 |
( 4.36) |
Отметим, что данную процедуру можно распространить на случай большего количества слоев (4.37).
 |
( 4.37) |
2. Как разбить множество пикселей на слои и определить движение каждого слоя? Процедура разбиения на слои состоит из нескольких шагов:
- Оценивание движения с использованием оптического потока и аффинной модели для набора неперекрывающихся блоков (рис.4.4, а), полученных в результате разбиения исходного изображения. Данная операция выполняется независимо для каждого кадра из подмножества изображений.
- Кластеризация полученных оценок с помощью метода k-средних (рис.4.4, b). Кластеризация также осуществляется независимо для каждого изображения. Каждый кластер определяет сегмент, отвечающий некоторому слою изображения.
- Применение медианной фильтрации для получения смешанных слоев, устойчивых к незначительным изменениям интенсивности, а также для выявления перекрытий между слоями (рис.4.4, c).
Впоследствии подобная схема была распространена на случай стерео. В более поздних работах, связанных с определением многослойного движения, рассмотренный подход модифицируется в части выделения слоев, например, для цветных изображений выполняется привычная сегментация и выполняется оценивание движения каждого сегмента в отдельности.

![Пример представления изображения в виде набора слоев [15]](/EDI/16_08_14_2/1408137470-25747/tutorial/1179/objects/4/files/04_03.jpg)
![Пример выделения слоев [14]](/EDI/16_08_14_2/1408137470-25747/tutorial/1179/objects/4/files/04_04.jpg)
 "
"