|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Лекция 3: Детекторы и дескрипторы ключевых точек. Алгоритмы классификации изображений. Задача детектирования объектов на изображениях и методы её решения
1. Алгоритмы детектирования ключевых точек
Презентацию к лекции Вы можете скачать здесь.
1.1 Детектор Моравеца
Одним из наиболее распространенных типов особых точек являются углы на изображении [104], т.к. в отличие от ребер углы на паре изображений можно однозначно сопоставить. Расположение углов можно определить, используя локальные детекторы. Входом локальных детекторов является черно-белое изображение. На выходе формируется матрица с элементами, значения которых определяют степень правдоподобности нахождения угла в соответствующих пикселях изображения. Далее выполняется отсечение пикселей со степенью правдоподобности, меньшей некоторого порога. Для оставшихся точек принимается, что они являются особыми.
Детектор Моравеца (Moravec) [148] является самым простым детектором
углов. Автор данного детектора предлагает измерять изменение
интенсивности пикселя  посредством смещения небольшого
квадратного окна с центром в
посредством смещения небольшого
квадратного окна с центром в  на один пиксель в каждом из восьми
принципиальных направлений (2 горизонтальных, 2 вертикальных и 4
диагональных). Размер окна обычно выбирается равным
на один пиксель в каждом из восьми
принципиальных направлений (2 горизонтальных, 2 вертикальных и 4
диагональных). Размер окна обычно выбирается равным 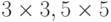 или
или
 пикселей. Детектор работает в несколько шагов:
пикселей. Детектор работает в несколько шагов:
- Для каждого направления смещения
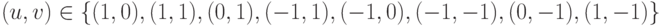 вычисляется
изменение интенсивности:
где
вычисляется
изменение интенсивности:
где
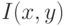 – интенсивность пикселя с координатами
– интенсивность пикселя с координатами  в исходном
изображении.
в исходном
изображении. - Строится карта вероятности нахождения углов в каждом пикселе
изображения посредством вычисления оценочной функции
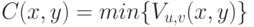 . По существу определяется направление,
которому соответствует наименьшее изменение интенсивности, т.к.
угол должен иметь смежные ребра.
. По существу определяется направление,
которому соответствует наименьшее изменение интенсивности, т.к.
угол должен иметь смежные ребра. - Отсекаются пиксели, в которых значения оценочной функции ниже некоторого порогового значения.
- Удаляются повторяющиеся углы с помощью процедуры NMS (non- maximal suppression) [85]. Все полученные ненулевые элементы карты соответствуют углам на изображении.
Основными недостатками рассматриваемого детектора являются отсутствие инвариантности к преобразованию типа "поворот" и возникновение ошибок детектирования при наличии большого количества диагональных ребер. Очевидно, что детектор Моравеца обладает свойством анизотропии в 8 принципиальных направлениях смещения окна.
1.2. Детектор Харриса и Стефана
Детектор Харриса (Harris) [105, 104, 109, 149] строится на основании детектора Моравеца и является его улучшением, т.к. для него характерна анизотропия по всем направлениям. Харрис и Стефан (Stephen) вводят в рассмотрение производные по некоторым принципиальным направлениям, раскладывают функцию интенсивности в ряд Тейлора:
![I(x+u+a,y+v+b)\approx I(x+a,y+b)+u \frac {\delta I} {\delta x}+v \frac {\delta I} {\delta y} \\ =I(x+a,y+b)+\left[ \frac {\delta I} {\delta x}\,\,\,\frac {\delta I} {\delta y} \right]\,\begin{bmatrix}
u \\
v
\end{bmatrix}.](/sites/default/files/tex_cache/ea86851e968ebca9f80cbed9415e2b75.png)
Как следствие, изменение интенсивности 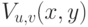 в каждом пикселе
можно рассматривать как функцию следующего вида:
в каждом пикселе
можно рассматривать как функцию следующего вида:
![V_{u,v}(x,y) = \sum_{\forall a,b, расположенных\;в\;окне} {\left( \left[ \frac{\partial I}{\partial x}\frac{\partial I}{\partial y} \right] \begin{bmatrix} u \\ v \end{bmatrix} \right)^2}](/sites/default/files/tex_cache/b03348086fc54bc2cca5caac7494fd0d.png)
![= \sum_{\forall a,b, расположенных\;в\;окне} {[u\;v] \begin{bmatrix} \frac{\partial I}{\partial x} \\ \frac{\partial I}{\partial y} \end{bmatrix} \left[ \frac{\partial I}{\partial x}\frac{\partial I}{\partial y} \right] \begin{bmatrix} u \\ v \end{bmatrix}](/sites/default/files/tex_cache/468eed952947d8875bbdd5d317807f6e.png)
![= [u\;v] \left(\sum_{\forall a,b, расположенных\;в\;окне} { \begin{bmatrix} \frac{\partial I}{\partial x} \\ \frac{\partial I}{\partial y} \end{bmatrix} \left[ \frac{\partial I}{\partial x}\frac{\partial I}{\partial y} \right]\right) \begin{bmatrix} u \\ v \end{bmatrix}](/sites/default/files/tex_cache/8f64c1d6e79a3e6e9abadb74ed9205f1.png)
![[u\;v]A_{u,v}(x,y)\begin{bmatrix} u \\ v \end{bmatrix}](/sites/default/files/tex_cache/ed1d7ca1c228fe975425a8332bd98cb8.png)
В матрице Харриса  (автокорреляционная матрица), как правило,
выбирают взвешенную свертку производных c весовыми коэффициентами
Гауссова окна (окно размером
(автокорреляционная матрица), как правило,
выбирают взвешенную свертку производных c весовыми коэффициентами
Гауссова окна (окно размером  пикселя с коэффициентами 0.04, 0.12,
0.04, 0.12, 0.36, 0.12, 0.04, 0.12, 0.04 – представление по строкам). Отметим,
что матрица Харриса симметричная и положительно полуопределенная.
Вычисляя собственные значения полученной матрицы [105], точки
изображения можно классифицировать на ребра и углы:
пикселя с коэффициентами 0.04, 0.12,
0.04, 0.12, 0.36, 0.12, 0.04, 0.12, 0.04 – представление по строкам). Отметим,
что матрица Харриса симметричная и положительно полуопределенная.
Вычисляя собственные значения полученной матрицы [105], точки
изображения можно классифицировать на ребра и углы:
- если оба собственных числа автокорреляционной матрицы достаточно большие, т.е. небольшой сдвиг окна приводит к значительным изменениям интенсивности, то пиксель классифицируется как угол;
- если одно собственное число значительно больше другого, то это означает, что окно было сдвинуто перпендикулярно выступу, поэтому пиксель принадлежит ребру;
- если собственные значения близки к нулю, тогда текущий пиксель не содержит ни углов, ни ребер.
Детектор Харриса по сравнению с ранее рассмотренным детектором требует большего количества вычислений за счет необходимости построения сверток с Гауссовым ядром. При этом он достаточно восприимчив к шумам. Подавить шумы позволяет увеличение размера Гауссова окна, но это приводит к значительным вычислительным расходам, поэтому необходимо находить компромисс между качеством работы алгоритма и количеством выполняемых операций. Детектор Харриса обладает свойством анизотропии вдоль горизонтального и вертикального направлений, т.к. автокорреляционная матрица содержит первые производные только вдоль указанных направлений. По сравнению со своим предшественником данный детектор инвариантен относительно поворота, количество ошибок детектирования углов не велико за счет введения свертки с Гауссовыми весовыми коэффициентами. Результаты детектирования значительно меняются при масштабировании изображения. Впоследствии возникают модификации детектора Харриса, которые учитывают вторые производные функции интенсивности (например, детектор Харриса-Лапласа (Harris-Laplace) [78]).
1.3. Детектор MSER’s
При разработке детектора MSER (Maximally Stable Extremal Regions, Matas и др., 2002) решается проблема инвариантности особых точек при масштабировании изображения. Детектор [19, 104, 75, 109] выделяет множество различных регионов с экстремальными свойствами функции интенсивности внутри региона и на его внешней границе.
Рассмотрим идею алгоритма для случая черно-белого изображения.
Представим все возможные отсечения изображения. В результате получим
набор бинарных изображений при разных значениях порога
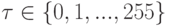 (пиксель, интенсивность которого меньше порога считаем
черным, в противном случае, белым). Таким образом, строится пирамида, у
которой на начальном уровне, соответствующем минимальному значению
интенсивности, находится белое изображение, а на последнем уровне,
отвечающем максимальному значению интенсивности, – черное. Если в
некоторый момент происходит движение, то на белом изображении
появляются черные пятна, соответствующие локальным минимумам
интенсивности. С увеличением порога пятна начинают разрастаться и
сливаться, в конечном итоге образуя единое черное изображение. Такая
пирамида позволяет построить множество связных компонент,
соответствующих белым областям, – регионов с максимальным значением интенсивности. Если инвертировать бинарные изображения в пирамиде, то
получим набор регионов с минимальным значением интенсивности. Схема
алгоритма состоит из нескольких этапов:
(пиксель, интенсивность которого меньше порога считаем
черным, в противном случае, белым). Таким образом, строится пирамида, у
которой на начальном уровне, соответствующем минимальному значению
интенсивности, находится белое изображение, а на последнем уровне,
отвечающем максимальному значению интенсивности, – черное. Если в
некоторый момент происходит движение, то на белом изображении
появляются черные пятна, соответствующие локальным минимумам
интенсивности. С увеличением порога пятна начинают разрастаться и
сливаться, в конечном итоге образуя единое черное изображение. Такая
пирамида позволяет построить множество связных компонент,
соответствующих белым областям, – регионов с максимальным значением интенсивности. Если инвертировать бинарные изображения в пирамиде, то
получим набор регионов с минимальным значением интенсивности. Схема
алгоритма состоит из нескольких этапов:
- Отсортируем множество всех пикселей изображения в порядке возрастания/убывания интенсивности. Отметим, что такая сортировка возможна за время, пропорциональное количеству пикселей.
- Построим пирамиду связных компонент. Для каждого пикселя отсортированного множества выполним последовательность действий:
- обновление списка точек, входящих в состав компоненты;
- обновление областей следующих компонент, в результате чего пиксели предыдущего уровня будут подмножеством пикселей следующего уровня.
- Выполним для всех компонент поиск локальных минимумов (находим пиксели, которые присутствуют в данной компоненте, но не входят в состав предыдущих). Набор локальных минимумов уровня соответствует экстремальному региону на изображении.
1.4. Детектор FAST
Описанные ранее детекторы определяют особых точек на изображении, в частности, углов, применяя некоторую модель или алгоритм напрямую к пикселям исходного изображения. Альтернативный подход состоит в том, чтобы использовать алгоритмы машинного обучения для тренировки классификатора точек на некотором множестве изображений. FAST- детектор (Features from Accelerated Test) [96, 109] строит деревья решений для классификации пикселей.
Для каждого пикселя p изображения рассматривается окружность с центром в этой точке, которая вписана в квадрат со стороной 7 пикселей (Рис3.1). Окружность проходит через 16 пикселей окрестности.
Каждый окрестный пиксель 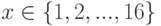 относительно центрального
относительно центрального
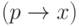 может находиться в одном из трех состояний:
может находиться в одном из трех состояний:
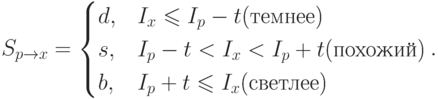
Выбирая x и вычисляя для каждого 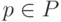 – множества всех пикселей
тренировочного набора изображений – разделяем множество P на три
подмножества
– множества всех пикселей
тренировочного набора изображений – разделяем множество P на три
подмножества 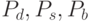 – множества точек, которые темнее, схожи и
светлее x соответственно. Далее выполняется построение дерева решений
согласно алгоритму, описанному в [93]. На каждом уровне дерева решений
множество, соответствующее узлу дерева, разбивается на подмножества
посредством выбора наиболее информативной точки (пикселя с
наибольшей энтропией). Построенное дерево решений в результате
используется для определения углов на тестовых изображениях.
– множества точек, которые темнее, схожи и
светлее x соответственно. Далее выполняется построение дерева решений
согласно алгоритму, описанному в [93]. На каждом уровне дерева решений
множество, соответствующее узлу дерева, разбивается на подмножества
посредством выбора наиболее информативной точки (пикселя с
наибольшей энтропией). Построенное дерево решений в результате
используется для определения углов на тестовых изображениях.


 "
"