|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Лекция 1: Основные цветовые модели, представление изображения, базовые операции над изображениями
Формирование изображений
Презентацию к лекции Вы можете скачать здесь.
Понятие цвета базируется на восприятии глазами человека электромагнитных волн в
определенном диапазоне частот. Человеческий глаз воспринимает длины волн  от 400 нм
(фиолетовый) до 700 нм (красный).
от 400 нм
(фиолетовый) до 700 нм (красный).
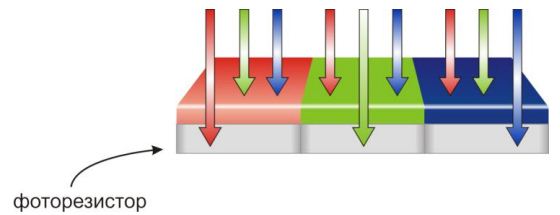
Формирование цифрового изображения в камере происходит следующим образом. Свет, отражённый от объектов сцены, проходит через линзу (или систему линз) объектива камеры и фокусируется на сенсоре, который состоит из фотоэлементов, покрытых светофильтрами. Таким образом, отдельные ячейки сенсора формируют разные цветовые каналы (рис.1.1) . Чаще всего используются RGB (red, green, blue) светофильтры.
Следует отметить, что в процессе формирования изображения возникают различные искажения, такие как: радиальная дисторсия из-за геометрии линзы, блики из-за переотражений в оптической системе, смазанные участки изображения из-за ошибок фокусировки или выдержки, затемненные или пересвеченные части изображения. Львиную часть этих искажений можно компенсировать с помощью методов цифровой обработки изображений, которая будет описана ниже.
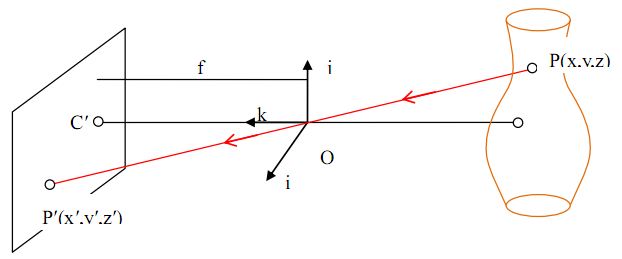
Для упрощения математического описания процесса формирования изображения часто применяют так называемую модель pinhole камеры, в которой считается, что световые лучи проходят через малое отверстие и попадают на сенсор (рис.1.2). При этом зависимость координат спроектированной точки и точки в мировой системе координат описывается уравнением перспективной проекции:
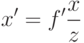

где 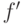 — фокусное расстояние,
— фокусное расстояние, 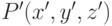 – координаты точки в системе координат камеры,
– координаты точки в системе координат камеры,
 – координаты точки в мировой системе координат.
– координаты точки в мировой системе координат.
Данные с элементов сенсора считываются в двухмерный массив, который называют растром.
Следует отметить, что компьютерное зрение используется не только для обработки и анализа изображений, сформированных цветными или черно-белыми камерами, но и устройствами, позволяющими видеть сцену в инфракрасном, миллиметровом и других диапазонах электромагнитного спектра.
Типы изображений
Элементом растра является пиксель.
Каждый пиксель может содержать одно или несколько значений в зависимости от типа изображения.
Определение. Цифровое изображение – это двумерный массив ![I[r,c]](/sites/default/files/tex_cache/b5c8321d24b47f5b348f35a858f77b4f.png) элементов (пикселей),
которые представляют собой одно или нескольких дискретных значений
элементов (пикселей),
которые представляют собой одно или нескольких дискретных значений
Определение. Бинарное изображение – это цифровое изображение ![B[r,c]](/sites/default/files/tex_cache/cba04903048246439a0d04dab0d9e0fa.png) , пиксели которого
принимают значения 0 или 1.
, пиксели которого
принимают значения 0 или 1.
Определение. Полутоновое (синонимы: серое, монохромное, черно-белое) изображение – это
цифровое изображение ![I[r,c]](/sites/default/files/tex_cache/b5c8321d24b47f5b348f35a858f77b4f.png) , у которого каждому пикселю соответствует одно значение
интенсивности (яркости).
, у которого каждому пикселю соответствует одно значение
интенсивности (яркости).
Определение. Мультиспектральное изображение – это цифровое изображение ![M[r,c]](/sites/default/files/tex_cache/e4a315c5c1d385e8eea3c5bc7cf8719b.png) , у которого
каждому пикселю соответствует вектор значений.
, у которого
каждому пикселю соответствует вектор значений.
У цветных изображений размерность этого вектора равна трем
В процессе решения задачи компьютерного зрения из исходного цветного изображения могут быть получены вспомогательные полутоновые или бинарные изображения. Для каждого класса изображений существуют свои методы обработки. Далее рассмотрим методы обработки бинарных изображений.

 "
"