Лекция 1: Основные цветовые модели, представление изображения, базовые операции над изображениями

Существуют и другие методы нахождения границ объектов на изображении. Пожалуй, наиболее популярным является метод Канни [4], реализацию которого можно найти в библиотеке OpenCV.

Кроме границ объектов в системах компьютерного зрения часто используются так называемые угловые точки, которые особенно важны для решения задачи слежения за объектом поскольку обладают свойством уникальности в некоторой окрестности.

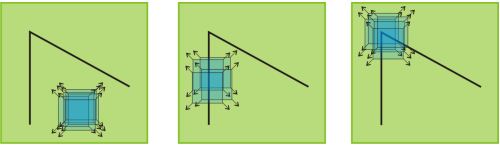
Угловая точка на изображении определяется как точка, некоторая окрестность которой не похожа на окрестности, полученные сдвигом этой точки в любом направлении. На рисунке ниже проиллюстрировано, что в однородной области нет изменений в окрестности точки в любом направлении, если точка на ребре, то нет изменений вдоль ребра, если точка угловая, то сдвиг окрестности точки в любом направлении повлечет изменение.

увеличить изображение
Рис. 1.9.

Математически меру схожести окрестностей можно выразить формулой

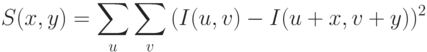
где 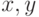– сдвиг окрестности, и - координаты пиксела в окрестности.

Рассмотрим метод представленный в работе [5] для определения положения угловых точек, который реализован в библиотеке OpenCV.

Считая, что и малы можно записать

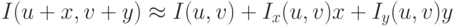
Тогда

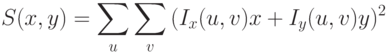
или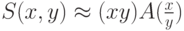

где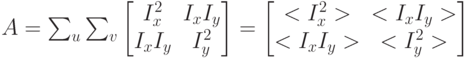

в угловых скобках записаны суммы квадратов производных и произведение частных производных.

Известно, что если матрица имеет большие собственные числа, то квадратичная функция изменяется во всех направлениях, то есть удовлетворяет условию угловой точки.

Таким образом, алгоритм имеет следующий вид:

Для каждого пиксела вычисляется минимальное собственное число матрицы

Находятся локальные максимумы в карте минимальных собственных чисел матрицы , анализируя окрестность 3 на 3.

Если величина найденного локального максимума превышает заданный порог, то координата этой точки записывается в выходной массив угловых точек.

Часто из-за ошибок экспозиции или из-за погрешностей в освещении изображение получается малоконтрастным. Рассмотрим алгоритм улучшения контраста, основанный на нахождении минимального и максимального значений яркости на изображении. Пусть 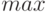– максимальное значение яркости, а – минимальное. Тогда новое значение пиксела можно записать 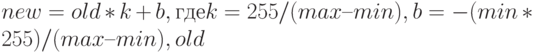– старое значение пиксела. Применяя данное преобразование ко всем пикселам изображения, контраст повысится, так как минимальная яркость будет 0, максимальная 255, а остальные значения линейно масштабируются. Ниже изображено исходное изображение и результирующее изображение с повышенным контрастом.

Рис. 1.10.

Другой популярный алгоритм повышения контраста – это эквализация гистограммы. Он состоит из следующих шагов:

1. Вычисляется гистограмма для исходного изображения
2. Значения бинов гистограммы нормализуются, так что их сумма равна 255
3. Вычисляется интеграл гистограммы .
4. Полученная интегральная кривая используется в качестве интерполяционной кривой по формул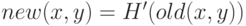е , где – новое значение пикселя в точке 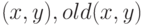– старое значение, 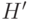– интегральная кривая.

Цветные изображения. Цветовые пространства

Если цветное изображение представить в виде трех одноканальных изображений, то для них применимы все рассмотренные методы обработки полутоновых изображений.

Следует отметить, что не все камеры формируют изображение в формате RGB, многие камеры видеонаблюдения вещают в формате YUV.

В этом формате яркостная составляющая Y выделена в отдельном канале. Две другие U и V несут цветовую информацию. Отметим, что человеческий глаз больше восприимчив к яркостной компоненте, поэтому основная обработка осуществляется для Y канала.

Переход из RGB в YUV и обратно осуществляется линейным преобразованием.

Обратное преобразование:

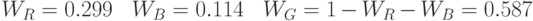
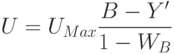
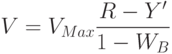
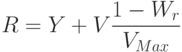
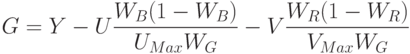
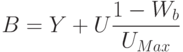
Существуют и другие удобные для анализа и обработки цветовые пространства, переход в которые из RGB может быть нелинейным. Например, рассмотрим пространство HSV, которое удобно тем, что его каналы имеют ясное семантическое значение: H – оттенок цвета (Hue), S – насыщенность цвета (Saturation), V – интенсивность цвета (Value). Таким образом, модифицируя канал S, мы можем управлять насыщенностью цветов на изображении.

Ниже представлены четыре изображения: первое – исходное RGB изображение, второе изображение, у которого в каждом пикселе повышена насыщенность S, третье – увеличена яркость (канал V), четвертое – модифицирован канал H, так что цвета поменяли оттенки.

увеличить изображение
Рис. 1.11.