|
Нахожу в тесте вопросы, которые в принципе не освещаются в лекции. Нужно гуглить на других ресурсах, чтобы решить тест, или же он всё же должен испытывать знания, полученные в ходе лекции? |
Лекция 1: Основные цветовые модели, представление изображения, базовые операции над изображениями
Обработка и анализ полутоновых изображений
Так же как и в случае бинарных изображений, работу с полутоновыми изображениями можно разделить на задачи фильтрации (удаление шумов, повышение чeткости, осветление тeмных участков) и задачи анализа (расчeт градиентов, поиск особых точек и границ объектов).
В процессе создания систем компьютерного зрения фильтрация изображения обычно предшествует извлечению более высокоуровневой информации о сцене, поэтому рассмотрим сначала методы фильтрации.
Линейная фильтрация является, пожалуй, самым часто применяемым методом обработки изображения из-за простоты реализации и скорости работы. Линейная фильтрация осуществляется с помощью дискретной свeртки изображения с заданным фильтром (ядро свeртки). Эту операцию можно представить формулой:
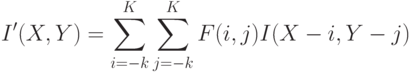
где  – исходное изображение,
– исходное изображение, 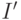 – выходное изображение,
– выходное изображение,  – заданный фильтр,
представленный изображением размером
– заданный фильтр,
представленный изображением размером 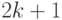 на
на 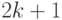 .
.
Рассмотрим различные фильтры:
1. Фильтр
не изменяет изображения.
2. Фильтр
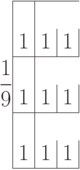
равномерно сглаживает изображение.
3. Фильтр
| 0.003 | 0.013 | 0.022 | 0.013 | 0.003 |
| 0.013 | 0.059 | 0.097 | 0.059 | 0.013 |
| 0.022 | 0.097 | 0.159 | 0.097 | 0.022 |
| 0.013 | 0.059 | 0.097 | 0.059 | 0.013 |
| 0.003 | 0.013 | 0.022 | 0.013 | 0.003 |
осуществляет фильтрацию по Гауссу.
Следует отметить, что для подсчета дискретной свертки на границе изображения можно, например, экстраполировать граничные пикселы за пределы изображения.
Фильтр
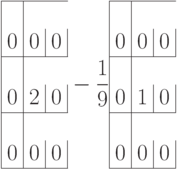
в противоположность фильтрам 2 и 3 не размывает, а делает изображение более четким, потому что, как видно из конструкции фильтра, в однородных частях изображение не изменяется, а в местах изменения яркости это изменение усиливается.
Рассмотрим еще один пример фильтра, на этот раз нелинейного, который повышает четкость изображения, например, в случае неправильно выбранного фокуса при съемке. Фильтрация осуществляется следующим образом:
Шаг 1: Из исходного изображения вычитается отфильтрованное с помощью гауссовского фильтра
![I1[i,j] = I[i,j] – (I * Gaussian)[i,j], I[i,j]](/sites/default/files/tex_cache/bd45733507ff65f9d3d99db833707dd6.png) – пиксель исходного изображения, * - операция свертки,
– пиксель исходного изображения, * - операция свертки, ![(I * Gaussian)[i,j]](/sites/default/files/tex_cache/e8b89e1d52901f518063f17c2a7da259.png) – пиксель отфильтрованного изображения.
– пиксель отфильтрованного изображения.
Шаг 2: Модуль изображения, полученного на шаге 1, сравнивается с некоторым порогом
(параметр алгоритма) и, если он меньше порога (пиксель находится в однородной области), то
изображение не изменяется, а если больше порога (это соответствует области изменения
яркости), то изменение яркости усиливается путем добавления к значению яркости ![I1[i,j]*k](/sites/default/files/tex_cache/85a64441c62c1f0b802c518f35b3dfe5.png) , где
, где
 – параметр алгоритма (чем он больше, тем контрастнее становятся границы объектов).
– параметр алгоритма (чем он больше, тем контрастнее становятся границы объектов).
![Result[i,j] = I[i,j] if | I1[i,j] | < = T,](/sites/default/files/tex_cache/9b4c85b10be234c66c750df7464aab26.png)
![Result[i,j] = I[i,j] + k * I1[i,j] if | I1[i,j] | > T](/sites/default/files/tex_cache/59a15c4e93bc104e32073a16fc983e02.png)
Другой пример нелинейного фильтра – это медианная фильтрация. Медианой набора чисел является число из набора, не меньшее половины чисел набора и не большее другой половины чисел набора. Для каждого пиксела изображения рассматривается его окрестность и вычисляется медиана яркостей пикселов из этой окрестности, значение которой и сохраняется в выходном изображении. Размер окна фильтрации зада?тся пользователем (обычно это окна 3x3 или 5x5).
Следует отметить, что медианная фильтрация лучше сохраняет границы изображенных объектов, чем линейная фильтрация, но является более ресурсоемкой по сравнению с линейной фильтрацией из-за необходимости осуществления операции сортировки.
Линейные фильтры можно также применять для выделения границ объектов. Рассмотрим фильтр Собеля:
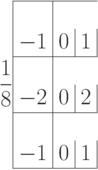
Видим, что он даст максимальное значение, когда справа от текущего пиксела лежит светлый объект, а слева темный (в идеале черный с нулевой яркостью). То есть фильтр по сути является разностной схемой для вычисления производной функции интенсивности по x. При этом соседние строчки принимаются во внимание для того, чтобы уменьшить влияние шума при вычислении производной.
Фильтр Собеля размером 3x3 для вычисления производной по y имеет вид:
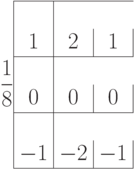
Для вычисления Лапласиана используется следующий фильтр:
Зная градиенты функции интенсивности и лапласиан, мы можем найти границы объектов, определяя их как точки с высокой нормой градиента (интенсивность резко изменяется на границе объекта) и нулевой второй производной (лапласиан = 0).
Пример нахождения границ объектов




 "
"