3. Применение теоремы Куна – Таккера для задачи выпуклого программирования
Выше была рассмотрена задача НП в виде (1.1), (1.2),
когда на переменные xj не накладывались
условия неотрицательности. Тем не менее часто в задачах
исследования операций приходится решать задачи, в которых
переменные xj по физическим условиям
должны удовлетворять условию  для всех
для всех  .
.
Покажем, как основные положения изложенной теории можно
распространить и на этот случай. Действительно, пусть задача НП
имеет вид:
 |
(
3.1)
|
при ограничениях
 |
(
3.2)
|
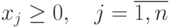 |
(
3.3)
|
Введем обозначения 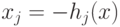 . Тогда ограничения (3.3) можно
записать в общем виде:
. Тогда ограничения (3.3) можно
записать в общем виде:
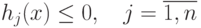 |
(
3.4)
|
Теперь задача задана в каноническом виде (1.1), (1.2).
Применим к ней теорему Куна-Таккера, для чего составим функцию
Лагранжа:
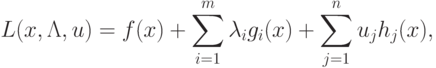 |
(
3.5)
|
где

- множители, связанные с ограничениями
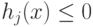
. Условия теоремы Куна-Таккера для (3.5)
выглядят так:
или
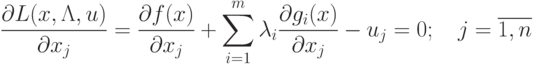 |
(
3.6)
|
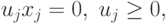 |
(
3.7)
|
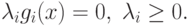 |
(
3.8)
|
Условия (3.5), (3.6), (3.7) можно записать в следующей
эквивалентной форме:
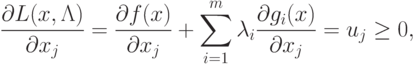 |
(
3.9)
|
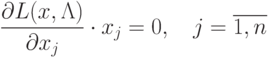 |
(
3.10)
|
Нетрудно увидеть, что условия (3.10) представляют собой условия дополняющей нежесткости
для ограничений неотрицательности.
Таким образом, найдены необходимые условия для оптимального
решения задачи НП вида (3.1) - (3.3), которые можно сформулировать
в следующей теореме.
Теорема 3.1. Пусть задача НП задана в виде
(3.1) - (3.3), а функции f(x) и g1(x), g2(x), ..., gm(x) дифференцируемы и выпуклы (по x ).
Вектор 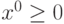 является оптимальным решением задачи НП тогда
и только тогда, когда существует такой вектор
является оптимальным решением задачи НП тогда
и только тогда, когда существует такой вектор  , что пара
, что пара 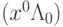 является седловой точкой функции Лагранжа, то есть выполняются такие условия:
является седловой точкой функции Лагранжа, то есть выполняются такие условия:
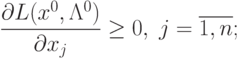 |
(
3.11)
|
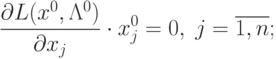 |
(
3.12)
|
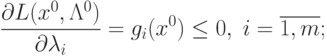 |
(
3.13)
|
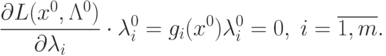 |
(
3.14)
|
Задача (3.1) - (3.3) при условиях, что все f()x, gi(x) - выпуклые функции, является задачей выпуклого программирования.
Ограничения 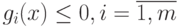 , определяют выпуклое
множество, и требуется найти минимум выпуклой функции f(x) на выпуклом множестве решений
, определяют выпуклое
множество, и требуется найти минимум выпуклой функции f(x) на выпуклом множестве решений 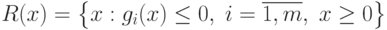 .
Рассмотрим задачу вогнутого программирования.
.
Рассмотрим задачу вогнутого программирования.
 |
(
3.15)
|
при ограничениях
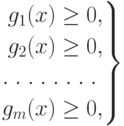 |
(
3.16)
|
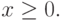 |
(
3.17)
|
где
f(x) и все функции
gi(x)
вогнуты по
x.
Покажем ее эквивалентность задаче выпуклого программирования
(3.1) - (3.3). Для этого обозначим 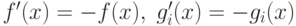 ,
и так как
,
и так как 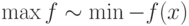 , то приходим к задаче:
, то приходим к задаче:
 |
(
3.18)
|
при ограничениях
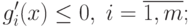 |
(
3.19)
|
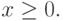 |
(
3.20)
|
Легко увидеть, что все функции 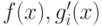 будут выпуклы по x,
а поэтому задача (3.18) - (3.20) - это задача выпуклого
программирования. Итак, эквивалентность задач (3.15) - (3.17)
и (3.1) - (3.3) установлена.
будут выпуклы по x,
а поэтому задача (3.18) - (3.20) - это задача выпуклого
программирования. Итак, эквивалентность задач (3.15) - (3.17)
и (3.1) - (3.3) установлена.
Нетрудно получить соответствующие признаки оптимальности для
задачи (3.15) - (3.17), аналогичные условиям (3.11) - (3.14).
Теорема 3.2. Пусть задача НП задана в виде
(3.15) - (3.17), а функции 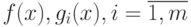 , - дифференцируемы . Для того чтобы вектор x0 являлся оптимальным
решением этой задачи, необходимо, чтобы существовал такой вектор
, - дифференцируемы . Для того чтобы вектор x0 являлся оптимальным
решением этой задачи, необходимо, чтобы существовал такой вектор  , для которого
выполнялись бы такие условия:
, для которого
выполнялись бы такие условия:
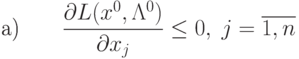 |
(
3.21)
|
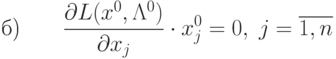 |
(
3.22)
|
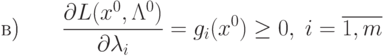 |
(
3.23)
|
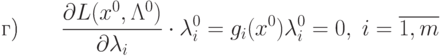 |
(
3.24)
|
Если функции 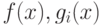 вогнуты, то условия (3.21) - (3.24) оказываются и достаточными.
вогнуты, то условия (3.21) - (3.24) оказываются и достаточными.
 для всех
для всех  .
.

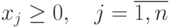
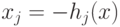 . Тогда ограничения (3.3) можно
записать в общем виде:
. Тогда ограничения (3.3) можно
записать в общем виде: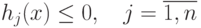
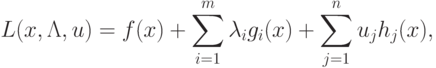
 - множители, связанные с ограничениями
- множители, связанные с ограничениями 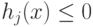 . Условия теоремы Куна-Таккера для (3.5)
выглядят так:
. Условия теоремы Куна-Таккера для (3.5)
выглядят так: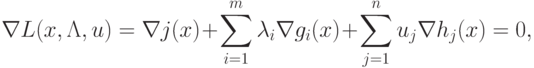
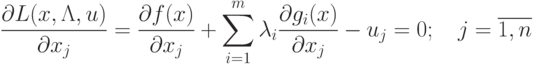
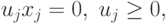
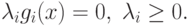
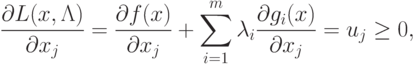
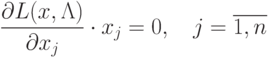
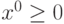 является оптимальным решением задачи НП тогда
и только тогда, когда существует такой вектор
является оптимальным решением задачи НП тогда
и только тогда, когда существует такой вектор  , что пара
, что пара 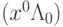 является седловой точкой функции Лагранжа, то есть выполняются такие условия:
является седловой точкой функции Лагранжа, то есть выполняются такие условия: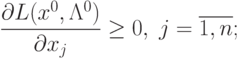
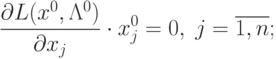
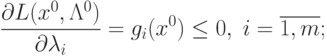
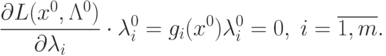
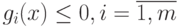 , определяют выпуклое
множество, и требуется найти минимум выпуклой функции f(x) на выпуклом множестве решений
, определяют выпуклое
множество, и требуется найти минимум выпуклой функции f(x) на выпуклом множестве решений 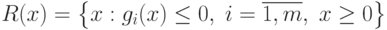 .
Рассмотрим задачу вогнутого программирования.
.
Рассмотрим задачу вогнутого программирования.
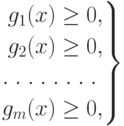
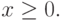
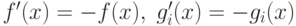 ,
и так как
,
и так как 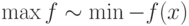 , то приходим к задаче:
, то приходим к задаче:
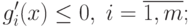
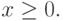
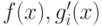 будут выпуклы по x,
а поэтому задача (3.18) - (3.20) - это задача выпуклого
программирования. Итак, эквивалентность задач (3.15) - (3.17)
и (3.1) - (3.3) установлена.
будут выпуклы по x,
а поэтому задача (3.18) - (3.20) - это задача выпуклого
программирования. Итак, эквивалентность задач (3.15) - (3.17)
и (3.1) - (3.3) установлена.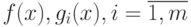 , - дифференцируемы . Для того чтобы вектор x0 являлся оптимальным
решением этой задачи, необходимо, чтобы существовал такой вектор
, - дифференцируемы . Для того чтобы вектор x0 являлся оптимальным
решением этой задачи, необходимо, чтобы существовал такой вектор  , для которого
выполнялись бы такие условия:
, для которого
выполнялись бы такие условия: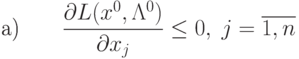
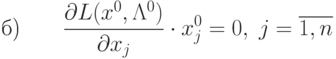
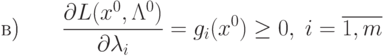
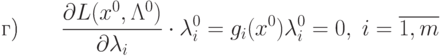
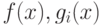 вогнуты, то условия (3.21) - (3.24) оказываются и достаточными.
вогнуты, то условия (3.21) - (3.24) оказываются и достаточными.