Лекция 3: Математическое программирование. Линейное программирование. Виды задач линейного программирования. Постановка задач линейного программирования и исследование их структуры. Решение задач линейного программирования симплекс-методом
Задача о раскрое материалов. Пусть поступает в раскрой m различных материалов. Требуется изготовить из них k разных комплектующих изделий (комплектов) в количествах, пропорциональных величинам b1, b2, . , bk (условия комплектности). Пусть каждую единицу j -го материала j=1, ., m можно раскроить n различными способами, так что при использовании i -го способа раскроя, i=1, ., n получим аij единиц k -го изделия. Нужно определить такой план раскроя материалов, обеспечивающий максимальное количество комплектов, если имеющийся запас j -го материала составляет аj единиц.
Обозначим через xij количество единиц j -го материала, раскраиваемых i -м способом, а через x -общее количество изготавливаемых комплектов.
Математическая модель этой задачи имеет такой вид:
 |
( 3.8) |
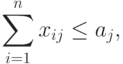 |
( 3.9) |
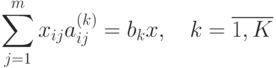 |
( 3.10) |
Условие (3.9) означает ограничение на запас j -го материала, а (3.10) - условие комплектности.
Оптимальные балансовые модели. Рассмотрим n -отраслевую балансовую модель с постоянными технологическими коэффициентами, задаваемыми матрицей затрат A=||aij||, где aij затраты продуктов i -й отрасли на производство единицы продукции j -й отрасли. Производственные мощности i -й отрасли ограничивают ее валовой выпуск величиной di (i = 1, ...,n), и пусть цена конечного продукта i -й отрасли составляет ci единиц.
Нужно определить оптимальный валовой выпуск продукции каждой отрасли, при котором будет достигнут максимальный суммарный выпуск конечного продукта в денежном выражении.
Обозначим вектор валовой продукции всех отраслей через x=[x1,.,xn], а вектор конечного продукта y=[y1,.,yn]. Тогда yi - объем продукции i -й отрасли, идущего на накопление.
Между векторами x и y существует следующая связь:
x = Ax+y,
где Ax - продукт, расходуемый на потребление. Отсюда
y=x [E-А], x=[E-A]-1y
Математическая модель этой задачи имеет вид
максимизировать cTy
при условиях
![x=[E-A]^{-1}y \leq d , \; y \geq 0;](/sites/default/files/tex_cache/95573f4f841250d8fd77c148a22706f2.png)
Кроме того, в этой задаче можно дополнительно использовать такие, например, ограничения на конечные продукты:
а) y1:y2:.:yn=b1:b2:.:bn -условие комплектности;
б) 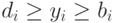 - условие ограниченности выпуска
конечного продукта.
- условие ограниченности выпуска
конечного продукта.
Форма записи задачи ЛП. Задачу линейного программирования можно сформулировать так:
 |
( 3.11) |
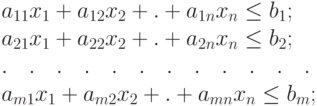 |
( 3.12) |
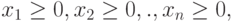 |
( 3.13) |
Ограничения (3.13) называют условиями неотрицательности переменных. В рассматриваемом случае все ограничения имеют вид неравенств.
Иногда они могут быть смешанными, то есть неравенства и равенства:
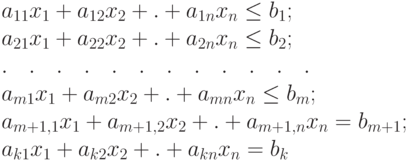 |
( 3.14) |
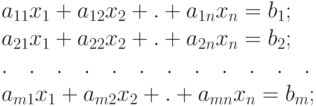 |
( 3.15) |
В матричной форме задача ЛП записывается следующим образом:
 |
( 3.16) |
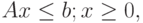 |
( 3.17) |
В векторной форме ограничения (3.14) записывают так:
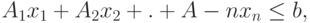 |
( 3.18) |
Допустимым множеством решений задачи (3.11)-(3.13) называется множество R(х) всех векторов x, удовлетворяющих условиям (3.12) и (3.13).
Множество R(х) представляет собой выпуклое многогранное множество или выпуклый многогранник.
Решение x0 называется оптимальным, если оно удовлетворяет условию

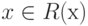 .
.Поскольку поиск 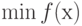 эквивалентен поиску
эквивалентен поиску ![\mах [-f(х)]](/sites/default/files/tex_cache/530099ad05cdf621d8bde2e76a4fb3e8.png) ,
то задачу ЛП всегда можно свести к эквивалентной задаче максимизации.
,
то задачу ЛП всегда можно свести к эквивалентной задаче максимизации.
