|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Алгоритмы вычисления размерностных многочленов
Другой способ вычисления размерностного
многочлена  для
для 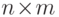 -матрицы
-матрицы  состоит в следующем. Для
состоит в следующем. Для  можно
вычислять
многочлен
можно
вычислять
многочлен  , пользуясь алгоритмом A9. Пусть
, пользуясь алгоритмом A9. Пусть  . В
этом случае применяем к
. В
этом случае применяем к  соотношение (12.3), в
котором
соотношение (12.3), в
котором  -
строка с максимальным значением элемента в первом столбце
матрицы
-
строка с максимальным значением элемента в первом столбце
матрицы  .
(Тривиальные случаи: если
.
(Тривиальные случаи: если  , то
, то 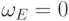 ;
если
;
если 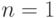 , применяем
алгоритм (12.3).) Легко видеть, что
число нулевых столбцов в матрице
, применяем
алгоритм (12.3).) Легко видеть, что
число нулевых столбцов в матрице  (см. (12.3)) больше, чем
в матрице
(см. (12.3)) больше, чем
в матрице  , и число строк в каждой из
матриц
, и число строк в каждой из
матриц  ,
,  меньше чем в
меньше чем в  .
Затем применяем описанную процедуру к
матрице
.
Затем применяем описанную процедуру к
матрице  и т.д., пока не получим матрицу,
размерностный
многочлен которой можно вычислить по алгоритму A9. В результате этого
процесса мы получаем представление требуемого
многочлена
и т.д., пока не получим матрицу,
размерностный
многочлен которой можно вычислить по алгоритму A9. В результате этого
процесса мы получаем представление требуемого
многочлена  в виде
линейной комбинации
многочленов
в виде
линейной комбинации
многочленов  (со
сдвинутыми аргументами),
таких, что каждая матрица
(со
сдвинутыми аргументами),
таких, что каждая матрица 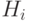 имеет ровно
имеет ровно  строк и
число ее нулевых
столбцов на один больше, чем в
строк и
число ее нулевых
столбцов на один больше, чем в  .
Многочлен
.
Многочлен 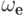 и некоторые из
многочленов
и некоторые из
многочленов 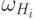 вычисляются по алгоритму A9 (в тех
случаях, когда этот алгоритм нужно применять в соответствии с вышеприведенными
рассуждениями). Для вычисления остальных
многочленов
вычисляются по алгоритму A9 (в тех
случаях, когда этот алгоритм нужно применять в соответствии с вышеприведенными
рассуждениями). Для вычисления остальных
многочленов 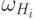 снова
применяем соотношение (12.3) и продолжаем в том же духе. Заметим, что
если первый столбец в матрице
снова
применяем соотношение (12.3) и продолжаем в том же духе. Заметим, что
если первый столбец в матрице  нулевой и
нулевой и  , то
число операций в
вычислении
, то
число операций в
вычислении 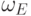 по предлагаемой схеме совпадает с числом
операций при
вычислении размерностного многочлена
по предлагаемой схеме совпадает с числом
операций при
вычислении размерностного многочлена  -матрицы.
Кроме того,
если
-матрицы.
Кроме того,
если  -
-  -матрица, то все ее строки
кроме той, которая
содержит элемент
-матрица, то все ее строки
кроме той, которая
содержит элемент  , являются
лишними, так что
вычисление размерностного многочлена по формуле
, являются
лишними, так что
вычисление размерностного многочлена по формуле 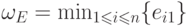 требует
требует 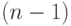 операцию. Таким образом,
если
операцию. Таким образом,
если  обозначает число элементарных операций (сложение,
сравнение или умножение)
необходимых для вычисления размерностного
многочлена
обозначает число элементарных операций (сложение,
сравнение или умножение)
необходимых для вычисления размерностного
многочлена  матрицы
матрицы  размера
размера 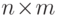 , то
, то  . Поскольку
. Поскольку 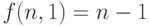 , имеем
, имеем

 .
.
Символ 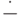 , которым мы пользуемся в алгоритме A12, обозначает следующую операцию на
векторах:
, которым мы пользуемся в алгоритме A12, обозначает следующую операцию на
векторах:

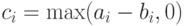 для
всех
для
всех 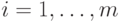 . При этом, если
. При этом, если  ,
то
,
то 
 обозначает
обозначает  -ю
координату элемента
-ю
координату элемента  .
.В заключение этого параграфа рассмотрим алгоритм вычисления размерностного многочлена, асимптотическая сложность которого меньше асимптотической сложности алгоритмов A9, A10, A11 и A12. Кроме того, представим алгоритм вычисления старшего коэффициента размерностного многочлена.
Пусть ![\mathbb Q[t]](/sites/default/files/tex_cache/4f86571a2c9dd7d0ff2b29aa9864c2e3.png) - кольцо многочленов над полем рациональных
чисел. Для
каждого
- кольцо многочленов над полем рациональных
чисел. Для
каждого 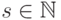 пусть
пусть  и
и  обозначают операторы, действующие на
обозначают операторы, действующие на ![\mathbb Q[t]](/sites/default/files/tex_cache/4f86571a2c9dd7d0ff2b29aa9864c2e3.png) следующим образом:
следующим образом:
 |
( 13.7) |

 для
всех
для
всех 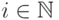 , то
, то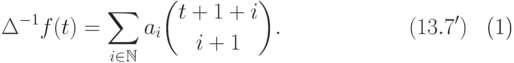
Отметим, что
операторы  и
и 
 ,
удовлетворяют следующему тождеству:
,
удовлетворяют следующему тождеству:
 |
( 13.8) |
![\Delta_1\Delta^{-1}=
\id_{\mathbb Q[t]}.](/sites/default/files/tex_cache/22b0bc331d09c19c88a000646a17d9ae.png)
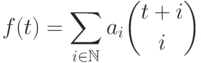
 для всех
для всех 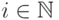 ,
и
,
и  для почти всех
для почти всех 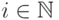 и пусть
и пусть  . По (11.4) имеем
. По (11.4) имеем![\begin{multiline*}
\Delta_s\Delta^{-1}f(t)
=\sum\limits_{i\in\mathbb N} a_i\left[\binom{t+i+1}{i+1}-\binom {t+i+1-s}{i+1}\right]
=\sum\limits_{i\in\mathbb N} a_i\sum\limits_{r=0}^{s-1} \binom {t+i+1-s+r}i
=\sum\limits_{i\in\mathbb N} a_i\sum\limits_{r=0}^{s-1} \binom {t+i-r}i\\
=\sum\limits_{r=0}^{s-1} \sum\limits_{i\in\mathbb N} a_i\binom {t+i-r}i
=\sum\limits_{r=0}^{s-1} f(t-r).
\end{multliine*}](/sites/default/files/tex_cache/b6abdb93801c4860d7ea3505b53436a0.png)
13.10. ЛЕММА. Пусть 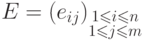 -
- 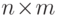 - матрица над
- матрица над 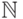 ,
,  и
и  . Через
. Через  обозначим матрицу, полученную
из
обозначим матрицу, полученную
из  удалением
удалением  -го столбца и всех строк с ненулевым
элементом в
-го столбца и всех строк с ненулевым
элементом в  -м столбце. Далее, пусть
-м столбце. Далее, пусть  -
- 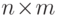 -матрица с элементами
-матрица с элементами

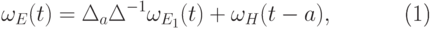 |
( 13.9) |
 ,
, 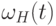 и
и 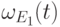 - размерностные многочлены матриц
- размерностные многочлены матриц  ,
,  и
и  соответственно.
соответственно.В частности, если

 , а все остальные
элементы первого столбца и первой строки равны нулю,
то
, а все остальные
элементы первого столбца и первой строки равны нулю,
то  .
.ДОКАЗАТЕЛЬСТВО.
Применяя формулу (12.2) к матрице  и
вектору
и
вектору  (
(  -
-  -я координата этого вектора), получаем
-я координата этого вектора), получаем

 и
вектору
и
вектору  (где 1 стоит на
(где 1 стоит на  -м
месте). По теореме 12.8(8)
получим
-м
месте). По теореме 12.8(8)
получим
 раз, получим равенство
раз, получим равенство
Теперь можно предложить следующую схему вычисления размерностного
многочлена  матрицы
матрицы  ,
основанную на формуле (13.9). Сначала, выбрав
вектор
,
основанную на формуле (13.9). Сначала, выбрав
вектор 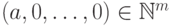 , где
, где  , и применив
лемму 13.10, сведем нашу задачу к
вычислению размерностного многочлена
матрицы
, и применив
лемму 13.10, сведем нашу задачу к
вычислению размерностного многочлена
матрицы  с
с  столбцом и размерностного многочлена
матрицы
столбцом и размерностного многочлена
матрицы  , такой,
что
, такой,
что 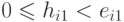
 . Для
определения
. Для
определения 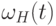 применим формулу
(13.9) (с матрицей
применим формулу
(13.9) (с матрицей  вместо
вместо  ) и продолжим
процесс до тех пор, пока
не получим представление
) и продолжим
процесс до тех пор, пока
не получим представление  в виде суммы размерностных
многочленов
матриц с
в виде суммы размерностных
многочленов
матриц с  столбцом и размерностного
многочлена
столбцом и размерностного
многочлена  ,
где
,
где  -
- 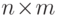 -матрица с нулевым первым
столбцом. Для вычисления
-матрица с нулевым первым
столбцом. Для вычисления  применяем описанную
процедуру ко второму столбцу и т. д.
применяем описанную
процедуру ко второму столбцу и т. д.

 .
.