|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Алгоритмы вычисления размерностных многочленов
13.1. ЛЕММА.
Пусть дана 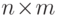 -матрица
-матрица
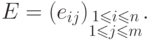
 мажорирует все строки этой матрицы,
т. е.
мажорирует все строки этой матрицы,
т. е.  больше любой строки матрицы
больше любой строки матрицы  или равен ей
(относительно порядка произведений на
или равен ей
(относительно порядка произведений на  ). Тогда
). Тогда 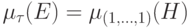 , где
, где  - матрица с элементами
- матрица с элементами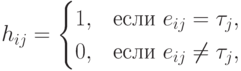
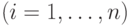 .
.ДОКАЗАТЕЛЬСТВО.
Пусть 
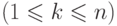 ,
,  и
и 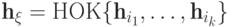 (
( 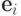 и
и 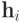 обозначают
обозначают  -е
строки матриц
-е
строки матриц  и
и  соответственно). Покажем, что
равенство
соответственно). Покажем, что
равенство 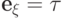 эквивалентно равенству
эквивалентно равенству  . Действительно, если
. Действительно, если 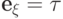 , то
, то 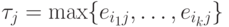
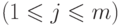 , так что для
каждого
, так что для
каждого 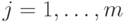 существует индекс
существует индекс  ,
такой, что
,
такой, что 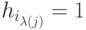 . Таким образом,
. Таким образом,  -й элемент
строки
-й элемент
строки  равен 1, следовательно,
равен 1, следовательно,  . Обратно, если
. Обратно, если 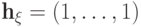 , то для каждого
, то для каждого 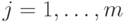 существует число
существует число 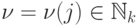 , такое, что
, такое, что  ,
т. е.
,
т. е. 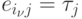 . Поэтому,
. Поэтому,  ,
следовательно,
,
следовательно, 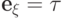 (так как элемент
(так как элемент  больше любой строки матрицы
больше любой строки матрицы  или равен ей). Таким образом,
или равен ей). Таким образом,
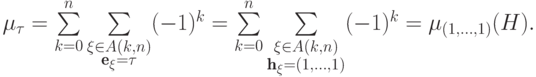
Рассмотрим свойства размерностных многочленов матриц, состоящих из 0 и 1
(такова, например, матрица  в лемме
13.1). Длякраткости будем писать
в лемме
13.1). Длякраткости будем писать 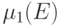 вместо
вместо 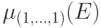 , где
, где  -
- 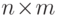 -матрица и
-матрица и  .
.
13.2. ЛЕММА. Пусть  -
- 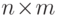 -матрица, состоящая из 0 и 1, и
-матрица, состоящая из 0 и 1, и  - ее многочлен Гильберта. Тогда
- ее многочлен Гильберта. Тогда 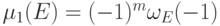 .
.
ДОКАЗАТЕЛЬСТВО. По (12.4) имеем
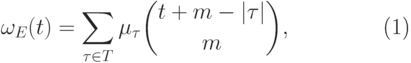 |
( 13.4) |

 , то
, то  . В этом случае
многочлен
. В этом случае
многочлен  обращается в нуль при
обращается в нуль при  , следовательно,
, следовательно,
Из леммы 13.2 следует, что
 |
( 13.5) |
 - многочлен Гильберта матрицы
- многочлен Гильберта матрицы  . Если
. Если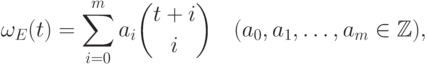
 , так что
, так что 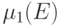 равно свободному
члену многочлена Гильберта
равно свободному
члену многочлена Гильберта  .
.13.3. ЛЕММА.
Пусть  -
- 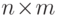 -матрица, состоящая из
0 и 1. Тогда
-матрица, состоящая из
0 и 1. Тогда
- если
 содержит нулевую строку, то
содержит нулевую строку, то  ;
; - если
 содержит нулевой столбец, то
содержит нулевой столбец, то  ;
; - значение
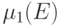 инвариантно относительно перестановки строк
(или столбцов) матрицы
инвариантно относительно перестановки строк
(или столбцов) матрицы  ;
; - если
 состоит из одной строки
состоит из одной строки  , то
, то 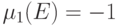 ;
; - если первая строка матрицы
 равна
равна 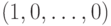 и первые элементы остальных строк
равны 0, то
и первые элементы остальных строк
равны 0, то  , где матрица
, где матрица  получена из
получена из  удалением первой строки и
первого столбца.
удалением первой строки и
первого столбца.
ДОКАЗАТЕЛЬСТВО.
Все утверждения леммы следуют из (13.5) и из доказанных выше свойств
размерностного многочлена
матрицы  .
.
(1) Если  содержит нулевую строку, то
содержит нулевую строку, то 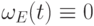 (см. теорему 12.8(6).
Применяя лемму 13.2, получаем
(см. теорему 12.8(6).
Применяя лемму 13.2, получаем  .
.
(2) Если каждый элемент  -го столбца матрицы
-го столбца матрицы  равен нулю
равен нулю  , то из формулы (13.2) следует, что
, то из формулы (13.2) следует, что  (действительно, в обозначениях
формулы (13.2)
(действительно, в обозначениях
формулы (13.2)  -ая координата любого вектора
-ая координата любого вектора 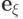
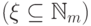 равна нулю, так что
равна нулю, так что 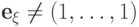 ни для
какого подмножества
ни для
какого подмножества 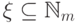 ).
).
(3) Очевидно, что перестановка строк (или столбцов) матрицы  не меняет значения
не меняет значения  , а, значит, и значения
, а, значит, и значения 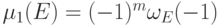 (см. утверждения (3) и (4) теоремы 12.8).
(см. утверждения (3) и (4) теоремы 12.8).
(4) Пусть  состоит из одной строки
состоит из одной строки 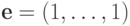 . Поскольку
. Поскольку

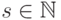 , имеем
, имеем
 .
.(5) По теореме 12.8(8) имеем  , следовательно,
, следовательно,  .
.
Пусть 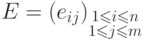 -
- 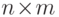 -матрица над
-матрица над 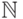 ,
,  - множество строк
матрицы
- множество строк
матрицы  и
и 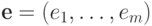 - элемент
множества
- элемент
множества  . Пусть
. Пусть 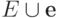 обозначает
обозначает 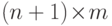 -матрицу,
полученную присоединением строки
-матрицу,
полученную присоединением строки  к матрице
к матрице  (без потери общности можно
предполагать, что
(без потери общности можно
предполагать, что  является
является 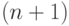 -й строкой матрицы
-й строкой матрицы 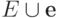 ). Следующая лемма устанавливает связь между
размерностными многочленами матриц
). Следующая лемма устанавливает связь между
размерностными многочленами матриц  и
и 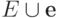 . Как и выше,
. Как и выше,  обозначает сумму
обозначает сумму 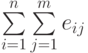 всех элементов
матрицы
всех элементов
матрицы  (в частности,
(в частности,  обозначает сумму всех координат элемента
обозначает сумму всех координат элемента 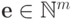 ).
).
