|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Наибольший общий делитель и последовательности полиномиальных остатков
Наибольший общий делитель. Определения и алгоритмы вычисления
В данном параграфе мы рассмотрим определение наибольшего общего делителя (НОД) двух элементов и алгоритмы его вычисления.
Пусть R — коммутативное кольцо с единицей,  . Мы говорим, что a делит b и пишем a|b, если существует элемент
. Мы говорим, что a делит b и пишем a|b, если существует элемент 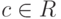 ,
такой, что
,
такой, что 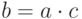 ; если такого элемента не существует, то мы говорим, что a не делит b, и пишем
; если такого элемента не существует, то мы говорим, что a не делит b, и пишем 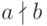 . Заметим, что определение
делимости зависит от рассматриваемого кольца. Так, например,
. Заметим, что определение
делимости зависит от рассматриваемого кольца. Так, например, 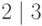 в поле рациональных чисел
в поле рациональных чисел  , но
, но 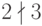 в кольце целых чисел
в кольце целых чисел 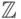 .
.
5.1. ОПРЕДЕЛЕНИЕ. Ненулевой элемент 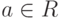 такой, что ab = 0
для некоторого
такой, что ab = 0
для некоторого  называется делителем нуля кольца R, а элемент
называется делителем нуля кольца R, а элемент 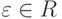 , такой, что
, такой, что  называется обратимым, или делителем
единицы, или единицей кольца R.
называется обратимым, или делителем
единицы, или единицей кольца R.
5.2. ОПРЕДЕЛЕНИЕ. Коммутативное кольцо с единицей и без де- лителей нуля называется областью целостности или просто областью.
5.3. ОПРЕДЕЛЕНИЕ. Пусть R — коммутативное кольцо с единицей. Элемент 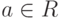 называется неприводимым, если из представления a = bc в виде произведения двух элементов кольца R, следует,
что хотя бы один из элементов b и c обратим в R.
называется неприводимым, если из представления a = bc в виде произведения двух элементов кольца R, следует,
что хотя бы один из элементов b и c обратим в R.
5.4. ОПРЕДЕЛЕНИЕ. Пусть R — коммутативное кольцо с едини-
цей. Идеал 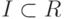 называется простым, если из
называется простым, если из 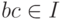 следует, что
хотя бы один из элементов b и c лежит в I.
следует, что
хотя бы один из элементов b и c лежит в I.
5.5. ОПРЕДЕЛЕНИЕ. Мы говорим, что идеал I порожден элементами b1, . . . , bn, и пишем I = (b1, . . . , bn), если 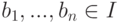 и любой
элемент
и любой
элемент 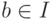 может быть записан в виде
может быть записан в виде 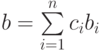 где
где 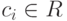 .
.
5.6. ОПРЕДЕЛЕНИЕ. Идеал I называется главным, если I = (b)
для некоторого элемента 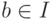 . Кольцо R называется кольцом главных идеалов, если любой идеал кольца R является главным.
. Кольцо R называется кольцом главных идеалов, если любой идеал кольца R является главным.
5.7. УПРАЖНЕНИЕ. Показать, что Z и k[x] — кольца главных идеалов, а ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) и k[x, y] — нет.
и k[x, y] — нет.
5.8. УПРАЖНЕНИЕ. Показать, что главный идеал (b) является простым тогда и только тогда, когда b — неприводимый элемент.
5.9. ОПРЕДЕЛЕНИЕ. Элементы a и b кольца R называются ассоциированными, если 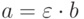 , где
, где  — единица (обратимый элемент)
кольца R.
— единица (обратимый элемент)
кольца R.
5.10. ОПРЕДЕЛЕНИЕ. Кольцо R называется факториальным или
кольцом с однозначным разложением на множители, если любой
элемент 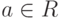 можно представить в виде
можно представить в виде  , где
, где  —
единица, а pi — неприводимые, причем если
—
единица, а pi — неприводимые, причем если 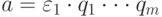 — другое такое разложение, то m = n и для любого индекса i существует
индекс j, такой, что pi ассоциировано с qj.
— другое такое разложение, то m = n и для любого индекса i существует
индекс j, такой, что pi ассоциировано с qj.
5.11. ЛЕММА. Пусть R — область главных идеалов. Если элемент 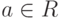 допускает разложение на неприводимые множители,
то это разложение однозначно в смысле предыдущего определения.
допускает разложение на неприводимые множители,
то это разложение однозначно в смысле предыдущего определения.
ДОКАЗАТЕЛЬСТВО оставим читателю в качестве упражнения.
5.12. УПРАЖНЕНИЕ. Показать, что ![\mathbb Z[x]](/sites/default/files/tex_cache/78229da1f420c78ec6c9078bb395c808.png) и k[x, y] — факториальные
кольца.
и k[x, y] — факториальные
кольца.
Сформулируем (без доказательства) теорему, которая позволяет получать новые факториальные кольца.
5.13. ТЕОРЕМА. Если R — факториальное кольцо, то кольцо многочленов R[x] также факториально.
Приведем пример нефакториального кольца.
5.14. ПРИМЕР. Кольцо ![\mathbb Z [\sqrt{-5}]](/sites/default/files/tex_cache/74ef6ea446e68a49065f71a74c9c7b72.png) — нефакториально. В частности,
— нефакториально. В частности, 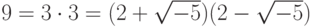 — два различных разложения числа 9 на неприводимые множители в этом кольце.
— два различных разложения числа 9 на неприводимые множители в этом кольце.
5.15. ОПРЕДЕЛЕНИЕ. Пусть R — коммутативное кольцо с единицей,  . Элемент
. Элемент  называется наибольшим общим делителем элементов a и b, если d | a, d | b и для любого другого элемента d', такого, что d' | a и d' | b выполняется соотношение d' | d.
называется наибольшим общим делителем элементов a и b, если d | a, d | b и для любого другого элемента d', такого, что d' | a и d' | b выполняется соотношение d' | d.
5.16. УПРАЖНЕНИЕ. Показать, что в кольце 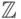 для любых целых
чисел a и b, не равных одновременно нулю, существует наибольшее
целое число, которое делит a и b, и это число является наибольших
общим делителем чисел a и b в смысле определения 5.15. Показать,
что определение 5.15 в кольце
для любых целых
чисел a и b, не равных одновременно нулю, существует наибольшее
целое число, которое делит a и b, и это число является наибольших
общим делителем чисел a и b в смысле определения 5.15. Показать,
что определение 5.15 в кольце 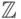 определяет НОД( a, b ) неоднозначно.
определяет НОД( a, b ) неоднозначно.
5.17. УПРАЖНЕНИЕ. Показать, что в кольце k[x] многочленов от одной переменной x над полем k для любых многочленов a и b, не равных одновременно нулю, существует многочлен наибольшей степени, который делит a и b, и этот многочлен является наибольшим общим делителем элементов a и b в смысле определения 5.15. Показать, что определение 5.15 в кольце k[x] определяет НОД( a, b ) неоднозначно.
Свойства НОД(a,b) в Z.
- НОД(a, a) = {a,-a}
- НОД(a, 0) = {a,-a}
- НОД(a, b) = НОД(b, a)
- НОД(c · a, c · b) = c · НОД(a, b)
- если НОД(a, c) = {1,-1} (в частности, если c = -1 ), то НОД(a, c · b) = НОД(a, b)
- НОД(a, b) = НОД(a - b, b)
- НОД(a, b) = НОД(b, r), где r — остаток от деления a на b
Используя различные комбинации этих свойств, можно получить
различные алгоритмы вычисления НОД(a, b) в кольце 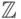 . Пользуясь
свойствами 3 и 5, можно свести задачу вычисления НОД в
. Пользуясь
свойствами 3 и 5, можно свести задачу вычисления НОД в 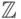 к
той же задаче для множества неотрицательных целых чисел и ограничиться представителем только положительного числа в качестве
результата. Например, используя свойства 1, 3, 6, можно получить
один из простейших алгоритмов вычисления НОД; используя свойства 1, 4, 5 с c = 2, получаем бинарный алгоритм вычисления НОД ; а используя свойства 2 и 7, получаем алгоритм Евклида нахождения наибольшего общего делителя натуральных чисел.
к
той же задаче для множества неотрицательных целых чисел и ограничиться представителем только положительного числа в качестве
результата. Например, используя свойства 1, 3, 6, можно получить
один из простейших алгоритмов вычисления НОД; используя свойства 1, 4, 5 с c = 2, получаем бинарный алгоритм вычисления НОД ; а используя свойства 2 и 7, получаем алгоритм Евклида нахождения наибольшего общего делителя натуральных чисел.
5.18. УПРАЖНЕНИЕ. Сформулировать перечисленные алгоритмы.
Евклидовы кольца.
Свойство 7 использует понятие "остаток от деления одного числа на другое" . На этом свойстве основан алгоритм Евклида, и распространение действия этого алгоритма на другие кольца достигается введением следующего определения.
5.19. ОПРЕДЕЛЕНИЕ. Область целостности R называется евклидовым кольцом, если каждому ненулевому элементу 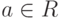 сопоставлено целое неотрицательное число g(a) со следующими свойствами:
сопоставлено целое неотрицательное число g(a) со следующими свойствами:
- если
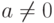 и
и  , то
, то  ;
; - для любых двух элементов
 , где
, где  существует представление
существует представление 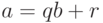 , в котором
, в котором 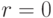 или
или 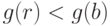 .
.
УПРАЖНЕНИЕ. Доказать, что следующие кольца являются евклидовыми:
- кольцо целых чисел
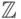 ;
; - кольцо многочленов k[x] от одной переменной над любым полем k ;
- любое поле k.
В качестве упражнения читателю предлагается доказать следующую теорему.
5.21. ТЕОРЕМА. Любое евклидово кольцо является кольцом главных идеалов, а следовательно, факториальным кольцом.
