|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Интегрирование полиномов и рациональных функций. Некоторые сведения из дифференциальной алгебры. Структурная теорема
Интегрирование полиномов и рациональных функций
Для решения простейших дифференциальных уравнений вида
 |
( 22.1) |
 из
некоторых классов. При этом обычно недостаточно четко задается класс
функций, в котором выбираются решения. Решение
из
некоторых классов. При этом обычно недостаточно четко задается класс
функций, в котором выбираются решения. Решение  уравнения (22.1)
определяется с точностью до произвольной константы и называется неопределенным интегралом или первообразной
функции
уравнения (22.1)
определяется с точностью до произвольной константы и называется неопределенным интегралом или первообразной
функции  .
.Прежде чем переходить к основной части данного раздела, напомним некоторые результаты математического анализа.
В этом разделе символом 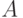 будем обозначать класс
функций, к которому
принадлежит функция
будем обозначать класс
функций, к которому
принадлежит функция  из правой части уравнения (22.1), а
символом
из правой части уравнения (22.1), а
символом 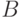 - класс функций, в котором выбирается решение.
- класс функций, в котором выбирается решение.
Прежде всего рассмотрим случай, когда 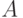 - кольцо полиномов
- кольцо полиномов ![K[x]](/sites/default/files/tex_cache/a77a9131b3530308247cff0e3c92321a.png) от
одной переменной над некоторым кольцом
от
одной переменной над некоторым кольцом  характеристики 0.
Предполагается,
что мы умеем выполнять арифметические операции в поле
характеристики 0.
Предполагается,
что мы умеем выполнять арифметические операции в поле  , в
частности,
, в
частности,  может совпадать с полем
может совпадать с полем  . В этом случае любое уравнение вида
(22.1) имеет
решение в этом же классе функций, и алгоритм его нахождения хорошо известен:
если
. В этом случае любое уравнение вида
(22.1) имеет
решение в этом же классе функций, и алгоритм его нахождения хорошо известен:
если 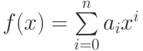 , то первообразная имеет вид
, то первообразная имеет вид 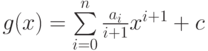 , где
, где  - произвольная
константа ( константа
интегрирования )
- произвольная
константа ( константа
интегрирования )
Следующим по сложности идет случай, когда 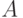 - поле
рациональных функций
- поле
рациональных функций  от одной переменной. Для простоты будем считать,
что поле
коэффициентов
от одной переменной. Для простоты будем считать,
что поле
коэффициентов  совпадает с полем рациональных чисел
совпадает с полем рациональных чисел  . Если класс
. Если класс 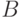 совпадает с
совпадает с 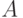 , то решение уравнения (22.1) существует
далеко не всегда.
Однако можно класс
, то решение уравнения (22.1) существует
далеко не всегда.
Однако можно класс 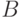 несколько расширить, добавив к нему
алгебраические
числа и операцию логарифмирования полиномов. Полученный класс будем обозначать
несколько расширить, добавив к нему
алгебраические
числа и операцию логарифмирования полиномов. Полученный класс будем обозначать  , и тогда любое уравнение вида
(22.1), где
, и тогда любое уравнение вида
(22.1), где  , разрешимо в классе
, разрешимо в классе 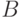 .
.
Напомним два метода решения уравнения (22.1) в этом случае.
I метод.
Пусть 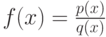 . Предположим, что мы умеем
находить
разложение функции
. Предположим, что мы умеем
находить
разложение функции  в сумму простейших
дробей:
в сумму простейших
дробей:  . Проинтегрировать сумму
почленно не представляет труда, пользуясь тем, что
. Проинтегрировать сумму
почленно не представляет труда, пользуясь тем, что
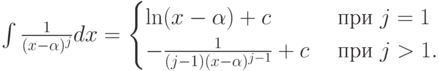
 , т.е корней
, т.е корней 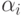 ее
знаменателя и разложение функции
ее
знаменателя и разложение функции  в сумму простейших
дробей.
в сумму простейших
дробей.II метод.
Как и прежде, предполагаем, что 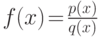 и что мы нашли все полюса
и что мы нашли все полюса 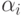 функции
функции  на комплексной плоскости.
Разложим в окрестности
каждого полюса
на комплексной плоскости.
Разложим в окрестности
каждого полюса 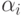 функцию
функцию  в ряд Лорана,
точнее, вычислим
главную часть разложения,
в ряд Лорана,
точнее, вычислим
главную часть разложения, 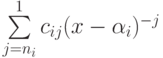 , где
, где 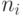 - порядок полюса в точке
- порядок полюса в точке 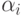 . Если
. Если  -
первообразная функции
-
первообразная функции  , то главная часть разложения функции
, то главная часть разложения функции  в
точке
в
точке 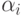 имеет
вид
имеет
вид
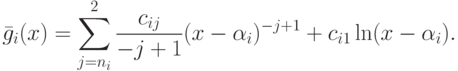
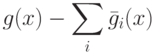
 . Для нахождения
этого полинома
можно также проинтегрировать главную часть разложения функции
. Для нахождения
этого полинома
можно также проинтегрировать главную часть разложения функции  в точке
в точке  .
.При реализации обоих методов основная трудность состоит в нахождении
полюсов 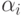 функции
функции  . При этом приходится работать в алгебраическом расширении
. При этом приходится работать в алгебраическом расширении  поля
поля  . Однако для записи ответа часто
оказывается
достаточным меньшее расширение поля
. Однако для записи ответа часто
оказывается
достаточным меньшее расширение поля  , чем
, чем  .
.
Читателю из курса анализа известно, что интегрирование рациональных функций с действительными коэффициентами осуществляется без алгебраического расширений поля констант (т. е. без использования комплексных чисел), а только с помощью логарифмов и арктангенсов рациональных функций. В действительности, в этих вычислениях неявно используются комплексные числа, поскольку арктангенсы выражаются через логарифмы с комплексными аргументами.
Вычисления в полях алгебраических чисел легко описываются теоретически, но при реализации на компьютере эти вычисления требуют весьма значительного времени счета и памяти для размещения результатов (особенно промежуточных). И время счета, и объем используемой памяти сильно зависят от степени расширения. В последнее время получены более эффективные алгоритмы интегрирования рациональных функций, позволяющие выполнять все вычисления, не прибегая к алгебраическим расширениям, большим чем то, которое требуется для записи ответа. Не рассматривая этот вопрос в полном объеме, приведем ниже метод Остроградского нахождения рациональной части интеграла рациональной функции.
Предположим, что рациональная функция  представлена в
виде суммы
полинома
представлена в
виде суммы
полинома 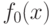 и правильной дроби (т. е. отношения двух
полиномов, в
котором степень числителя меньше степени знаменателя)
и правильной дроби (т. е. отношения двух
полиномов, в
котором степень числителя меньше степени знаменателя)  .
Мы можем
отдельно интегрировать полиномиальную
.
Мы можем
отдельно интегрировать полиномиальную 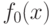 и рациональную
и рациональную  части
функции
части
функции  . Интеграл от
. Интеграл от 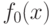 является полиномом,
и его вычисление не
представляет труда. Интеграл от
является полиномом,
и его вычисление не
представляет труда. Интеграл от  представляется в
виде суммы
правильной дроби
представляется в
виде суммы
правильной дроби 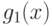 и логарифмической части
и логарифмической части 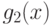 интеграла.
Логарифмическая часть получается от интегрирования правильных дробей, в
знаменателе которых стоят неприводимые полиномы (в первой степени). Сумма
таких дробей является правильной дробью, знаменатель
интеграла.
Логарифмическая часть получается от интегрирования правильных дробей, в
знаменателе которых стоят неприводимые полиномы (в первой степени). Сумма
таких дробей является правильной дробью, знаменатель  которой
свободен от квадратов и делит знаменатель исходной функции
которой
свободен от квадратов и делит знаменатель исходной функции  . Алгоритм
нахождения
. Алгоритм
нахождения  описан в параграфе "Разложение на свободные от
квадратов
множители". Как легко следует из первого метода интегрирования, рациональная
часть
описан в параграфе "Разложение на свободные от
квадратов
множители". Как легко следует из первого метода интегрирования, рациональная
часть 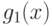 интеграла функции
интеграла функции  является
правильной дробью,
знаменатель
является
правильной дробью,
знаменатель 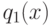 которой получается из знаменателя функции
которой получается из знаменателя функции  делением его на
делением его на  . Числитель
. Числитель 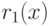 рациональной части однозначно
определяется условиями:
рациональной части однозначно
определяется условиями: 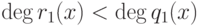 и
и  - правильная рациональная дробь со
знаменателем
- правильная рациональная дробь со
знаменателем  . Вычисление полинома
. Вычисление полинома 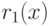 осуществляется
методом неопределенных
коэффициентов.
осуществляется
методом неопределенных
коэффициентов.
Два изложенных выше метода интегрирования рациональных функций обобщаются на
различные более общие классы функций. Для формулирования основных результатов
нам понадобится ввести некоторые определения. В частности, выше было
использовано обозначение 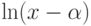 , где
, где  - алгебраическое
число. Ниже будет объяснено, что скрывается за этим обозначением.
- алгебраическое
число. Ниже будет объяснено, что скрывается за этим обозначением.
Хотя проблематика интегрирования в конечном виде возникла из математического и функционального анализа, описание удобнее давать в терминах дифференциальной алгебры.
