|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Логическое программирование
Правила образования формул
- Если
 —
—  -местный предикатный символ,
а
-местный предикатный символ,
а 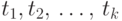 —
термы, то выражение
—
термы, то выражение  является формулой
(атомарной).
является формулой
(атомарной). - Если
 и
и  — формулы, то выражения
— формулы, то выражения ![[A \& B]](/sites/default/files/tex_cache/03ec7701eaa7aeb82e9dfa93c2fd6298.png) ,
, ![[A \vee B]](/sites/default/files/tex_cache/084cf8015f2fee3a51b7a60f64e45626.png) ,
, ![[A \to B]](/sites/default/files/tex_cache/b07d02acf6634ba0e52cb3f0786f9e24.png) и
и  являются формулами.
являются формулами. - Если
 — формула, а
— формула, а  — переменная,
то выражения
— переменная,
то выражения 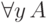 ,
, 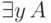 являются формулами.
являются формулами.
Замечания
- В правиле
 формула
формула  называется областью
действия соответствующего квантора, а все вхождения переменной
называется областью
действия соответствующего квантора, а все вхождения переменной  в атомарные подформулы формулы
в атомарные подформулы формулы  называются связанными.
называются связанными. - Переменная, имеющая вхождение в атомарную подформулу
формулы
 ,
не находящуюся в области действия соответствующего квантора, называется
свободной переменной формулы
,
не находящуюся в области действия соответствующего квантора, называется
свободной переменной формулы  . Конечно, одна и та же переменная
может иметь как связанные, так и свободные вхождения в формулу.
. Конечно, одна и та же переменная
может иметь как связанные, так и свободные вхождения в формулу. - Формула, не имеющая переменных со свободными вхождениями, называется предложением.
- Формулы, в которых имеются свободные вхождения переменных, трактуются как высказывательные формы, а предложения — как высказывания, истинностная оценка которых зависит от интерпретации входящих в них предикатных и функциональных символов в соответствии со смыслом логических связок и кванторов.
Пример.
Пусть нелогическая сигнатура состоит из трех символов  , где
, где  — двухместный предикат,
— двухместный предикат,  —
одноместная функция,
—
одноместная функция,  — двухместная функция, тогда
выражение
— двухместная функция, тогда
выражение

Рассмотрим следующую интерпретацию нашей сигнатуры. Пусть универсумом рассуждения будет множество точек плоскости, это означает, что значениями переменных являются точки. Далее, пусть
-
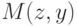 — точка, являющаяся серединой отрезка
— точка, являющаяся серединой отрезка 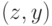 ,
, -
 — точка, симметричная точке
— точка, симметричная точке  относительно некоторой точки,
относительно некоторой точки, -
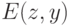 — предикат, означающий равенство
точек
— предикат, означающий равенство
точек  и
и  .
.
При такой интерпретации нелогических символов 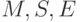 ,
приведенная выше формула есть утверждение о том, что середина
отрезка
,
приведенная выше формула есть утверждение о том, что середина
отрезка 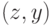 симметрична середине отрезка с концами,
симметричными точкам
симметрична середине отрезка с концами,
симметричными точкам 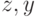 .
.
Очевидно, что это утверждение истинно.
Рассмотрим еще одну интерпретацию нашей сигнатуры. Пусть на этот раз
универсумом рассуждения будет множество действительных чисел, исключая
число  :
:
-
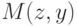 — произведение чисел
— произведение чисел 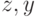 ,
, -
 — число, обратное числу
— число, обратное числу  ,
, -
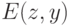 — "
— "  ".
".
Рассматриваемая нами формула является теперь утверждением о том, что для любых двух чисел из нашего универсума выполняется равенство
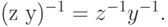
Очевидно, что это утверждение истинно. Нетрудно привести примеры интерпретаций, при которых наша формула ложна. Следующие примеры показывают, что существуют формулы, тождественно истинные, то есть истинные при любой интерпретации, а также тождественно ложные.
Примеры. Пусть  и
и  — одноместные
предикатные символы.
— одноместные
предикатные символы.
-
![\forall x [\neg P(x) \vee P(x)]](/sites/default/files/tex_cache/23910b6c3180d6a65a4549842eae2fc3.png) — тождественно
истинная формула.
— тождественно
истинная формула. -
![\forall x [\neg P(x) \& P(x)]](/sites/default/files/tex_cache/cde0d341d28efbd0ac07ebeb91dd9bb4.png) — тождественно ложная
формула.
— тождественно ложная
формула. -
![\forall x [P(x) \vee Q(x)]](/sites/default/files/tex_cache/db5f99a85c2cef5db14ea8c073952a9f.png) — истинность этой формулы
зависит от интерпретации предикатных символов
— истинность этой формулы
зависит от интерпретации предикатных символов  и
и  .
.
Если в формуле есть свободные переменные, то она получает конкретное истинностное значение при означивании этих переменных.
Формула называется выполнимой, если она истинна хотя бы при одной интерпретации.
Две формулы называются логически равносильными, если при любой интерпретации предикатных и функциональных символов и при любом означивании свободных переменных они имеют одно и то же истинностное значение.
Например, формулы
![\eq*{
\begin{gathered}
\forall x [P(x) \vee Q(x)],\\
[\forall x P(x) \vee \forall x Q(x)]
\end{gathered}
}](/sites/default/files/tex_cache/ebf1c2f2bc6c2f863a4c54cd715ab0fd.png)
не являются логически равносильными, а формулы
![\eq*{
\begin{gathered}
\forall x [P(x) \& Q(x)],\\
[\forall x P(x) \& \forall x Q(x)]
\end{gathered}
}](/sites/default/files/tex_cache/167e3c9911c99c47c23276ded496fd6b.png)
логически равносильны.
Логическую равносильность формул будем обозначать знаком 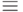 ,
например,
,
например,
![\eq*{
\forall x\, [P(x) \& Q(x)] \equiv [\forall x\, P(x) \& \forall x Q(x)].
}](/sites/default/files/tex_cache/8719583e7df20db4df4ed7a91405ad66.png)
Заметим, что в этом выражении фигурирует не одна формула, а две, соединенные знаком логической равносильности.

