Ленивые левосторонние и самоорганизующиеся кучи

Самоорганизующаяся куча

Самоорганизующаяся куча — это представление приоритетной очереди корневым деревом, операции с которым производятся аналогично операциям с левосторонней кучей, но без использования рангов. Длина правого пути из корня такого дерева в лист может быть произвольной, поэтому время выполнения всех операций в худшем случае есть , где — число элементов в очереди. Однако среднее время выполнения произвольных операций есть 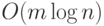, то есть время, приходящееся на одну операцию, как ни удивительно, является величиной . Для их реализации необходимо с каждым узлом дерева хранить элемент, его ключ, указатели на левое и правое поддеревья, то есть узлы представлять записями вида

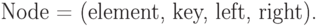
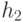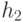Операция СЛИТЬ кучи и в одну кучу выполняется следующим образом. Правые пути двух исходных куч и сливаются в один путь, упорядоченный по правилам кучи, и этот путь становится левым путем результирующей кучи . Левые поддеревья узлов, попавших в результирующий левый путь, становятся правыми.

Операция ВСТАВИТЬ в кучу новый элемент производится посредством слияния кучи с кучей, содержащей единственный элемент . Таким образом, время выполнения этой операции равно времени выполнения операции СЛИТЬ.

Операция УДАЛИТЬ_ЭЛЕМЕНТ_С_МИНИМАЛЬНЫМ_КЛЮЧОМ производится посредством удаления корня кучи и слияния его левой и правой подкуч. Таким образом, вычислительная сложность этой операции равна вычислительной сложности операции СЛИТЬ.

Операция НАЙТИ_ЭЛЕМЕНТ_С_МИНИМАЛЬНЫМ_КЛЮЧОМ выполняется, очевидно, за время , так как этот элемент находится в корне.

Анализ времени выполнения операции СЛИТЬ. Поскольку время выполнения всех трудоемких операций определяется временем выполнения операции СЛИТЬ, остается проанализировать именно эту операцию. Очевидно, время ее выполнения пропорционально количеству узлов в правых путях исходных куч и 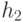. Длина такого пути в худшем случае может зависеть линейно от количества узлов в соответствующей куче. Таким образом, время выполнения операции СЛИТЬ есть величина 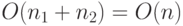, где , , 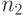— количества узлов в кучах , , 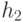, соответственно.

Нахождение суммарной оценки времени выполнения m операций СЛИТЬ. Введем определение. Узел назовем тяжелым, если количество узлов в его правом поддереве строго больше, чем в левом. Остальные узлы назовем легкими.

Определим потенциал коллекции куч как общее количество содержащихся в ней тяжелых узлов. Пусть 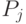— потенциал коллекции после выполнения -й операции.