| Россия, г. Москва |
Системы счисления. Перевод чисел из одной системы счисления в другую
Система счисления
Система счисления — совокупность приемов и правил для записи чисел цифровыми знаками.
Любая предназначенная для практического применения система счисления должна обеспечивать:
- возможность представления любого числа в рассматриваемом диапазоне величин;
- единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);
- простоту оперирования числами.
Типы систем счисления:
- позиционные,
- непозиционные.
Непозиционные системы счисления (СС) характеризуются тем, что для представления какого-либо числа используется определенный набор символов, который изменяется при изменении диапазона представляемых чисел. В качестве типичного примера непозиционной системы счисления обычно приводится римская система счисления, в которой для небольших чисел и коррекции чисел с большим значением используется символ I. Для представления больших чисел приходится вводить новые символы (V, X, C и т.д.).
В позиционных системах счисления значение единицы цифры каждого разряда числа имеет постоянный вес. Этот вес определяется позицией, которую разряд занимает по отношению к запятой:
234,5610 = 2*102 + 3*103 + 4*104 + 5*10-1 + 6*10-2
С этой точки зрения, римская система счисления не является чисто непозиционной, т.к., например, число IV равно четырем, а число VI – шести.
Любая позиционная система счисления характеризуется своим основанием.
Основание (базис) p-й позиционной системы счисления – количество знаков, или символов, используемых для изображения числа в данной системе:
-
p=10 ? {ai} = 0,1, …,9;
-
p=2 ? {ai} = 0,1;
-
p=5 ? {ai} = 0,1,2.3.4;
-
p=16 ? {ai} = 0, 1, …, 9, A, B, C, D, E, F;
-
p=q? {ai} = 0,1.,…,q-1
| Десятичное число | Эквиваленты в некоторых других системах счисления | |||
|---|---|---|---|---|
| p = 2 | p = 5 | p = 8 | p = 16 | |
| 0 | 0000 | 00 | 00 | 0 |
| 1 | 0001 | 01 | 01 | 1 |
| 2 | 0010 | 02 | 02 | 2 |
| 3 | 0011 | 03 | 03 | 3 |
| 4 | 0100 | 04 | 04 | 4 |
| 5 | 0101 | 10 | 05 | 5 |
| 6 | 0110 | 11 | 06 | 6 |
| 7 | 0111 | 12 | 07 | 7 |
| 8 | 1000 | 13 | 10 | 8 |
| 9 | 1001 | 14 | 11 | 9 |
| 10 | 1010 | 20 | 12 | A |
| 11 | 1011 | 21 | 13 | B |
| 12 | 1100 | 22 | 14 | C |
| 13 | 1101 | 23 | 15 | D |
| 14 | 1110 | 24 | 16 | E |
| 15 | 1111 | 30 | 17 | F |
| 16 | 10000 | 31 | 18 | 10 |
Для любой позиционной системы счисления основание изображается числом 10 в данной системе.
В общем виде число А в p-ной позиционной системе счисления представляется в виде:
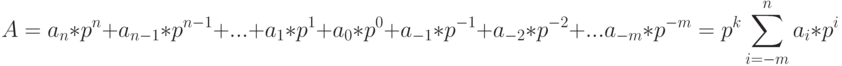 |
( 6.1) |
При k = Const получается число, носящее, в общем случае, название числа с фиксированной точкой, но имеющее две разновидности:
-
k=0: правильная дробь – число с фиксированной запятой, то есть правильную дробь
A = a-1*p-1+a-2*p-2+…+a-m*p-m
-
k=r: целое число – число с фиксированной точкой, то есть целое число
A = an*pn+an-1*pn-1+…+a1*p1+a0*p0
При k ?Const получается число с плавающей запятой.
Представление в виде числа с фиксированной точкой (или ее разновидности – с фиксированной запятой) влияет на диапазон представляемых чисел и их точность.
Микропроцессоры, которые в настоящее время служат основой для построения ЭВМ различных типов, содержат в своем составе как блоки, предназначенные для обработки целых чисел (СPU –CentralPointUnit), так и блоки для обработки чисел с плавающей запятой (FPU – FloatingPointUnit, в силу англоязычной специфики представления дробных чисел целая часть от дробной отделяется не запятой, а точкой). Представление чисел с плавающей запятой включает в себя порядок (целое число) и мантиссу (правильную дробь), которые обрабатываются в отдельных блоках FPU. Поэтому изучение особенностей представления и обработки каждого из типов чисел чрезвычайно важно для изучения устройства ЭВМ, выбора необходимого формата данных как с точки зрения требуемого диапазона, так и допустимой погрешности.
Обсуждение способов кодирования и различных алгоритмов обработки чисел мы будем проводить, в основном, на примере чисел с фиксированной запятой, так как именно в этом формате представляются мантиссы чисел с плавающей запятой, что сказывается на обработке чисел с плавающей запятой в целом. В свою очередь использование чисел с плавающей запятой играет в настоящее время весьма важную роль в процессе человеко-машинного общения, снимая с программиста во многих случаях обязанность по отслеживанию диапазона и точности используемых и получаемых данных.
К тому же числа с фиксированной запятой играют заметную самостоятельную роль в специализированных компьютерах, работающих в определенном диапазоне чисел, повышая при этом быстродействие таких вычислений, что особенно проявилось в ЭВМ второго и третьего поколений.
