| Россия, г. Москва |
Функционально-полные системы логических функций. Свойства логических функций
Полнота системы логических функций
Булева функция может быть представлена суперпозицией (совокупности) некоторого набора функций {f1, f2, ... fn}.
Система элементарных логических функций f1 … fm называется полной, если любую ФАЛ можно изобразить в виде суперпозиции функций f1 . . . fn.
Теорема. Пусть даны две системы логических функций:
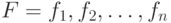 |
( 4.1) |
и
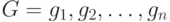 |
( 4.2) |
Если система (4.1) полна и каждая её функция может быть выражена как суперпозиция функций системы (4.2), тогда система (4.2) является полной.
Пример 4.1. Известно, система функций {И, ИЛИ, НЕ} является функционально полной (например, именно в этой системе логических функций можно представить её совершенные дизъюнктивную и конъюнктивную нормальные формы СДНФ, СКНФ). Отсюда следует, что система ФАЛ, состоящая из одной функции "Штрих Шеффера", также функционально полна, так как:
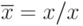

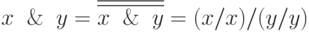
Правила перехода от представления ФАЛ в виде ДНФ к функции, представленной в базисе "Штрих Шеффера"
- если в ДНФ есть элементарные конъюнкции, имеющие ранг 1, то необходимо повысить их ранг путём выполнения эквивалентного преобразования: a = a & a или a = a & 1;
- в полученной ДНФ заменить все операции дизъюнкции и конъюнкции операциями "Штрих Шеффера";
- группы букв, соответствующие дизъюнктивным членам (элементарным конъюнкциям), заключить в скобки.
Правила перехода от представления ФАЛ в виде КНФ к функции, представленной в базисе "Стрелка Пирса"
- если в КНФ есть элементарные конъюнкции, имеющие ранг 1, то необходимо повысить их ранг путём выполнения эквивалентного преобразования: a = a V a или a = a V 0;
- в полученной КНФ заменить все операции дизъюнкции и конъюнкции операциями "Стрелка Пирса";
- группы букв, соответствующие конъюнктивным членам (элементарным дизъюнкциям), заключить в скобки.
Свойства логических функций
Рассмотрим основные свойства логических функций, которые позволят определить их состав, составляющий функционально полный набор.
Переключательной (логической) функцией, сохраняющей нуль, называется функция, которая на нулевом наборе аргументов, т.е. на наборе (0,0, ..., 0,0), равна нулю. Для переключательных функций, сохраняющих нуль, выполняется условие: f( 0,0, ..., 0,0 ) = 0.
Очевидно, что логических функций от n аргументов, сохраняющих ноль, будет ровно половина от всех возможных функций, то есть  .
.
Переключательной функцией, сохраняющей единицу, называется функция, которая на единичном наборе аргументов, т.е. на наборе (1,1, ..., 1,1), равна единице. Для переключательных функций, сохраняющих единицу, выполняется условие:f (1,1, ..., 1,1) = 1. Функций, обладающих этим свойством, будет также ровно половина: .
.
К одному из основных свойств логической функции относится ее принадлежность к классу самодвойственных функций. Чтобы рассмотреть это свойство разберем вначале несколько сопутствующих понятий.
Два набора аргументов называются противоположными, если все значения аргументов одного набора противоположны значениям аргументов другого набора. Чтобы получить противоположный набор, достаточно заменить в данном наборе нули единицами, а единицы нулями.
Для функции трех аргументов следующие пары наборов являются противоположными:
000 и 111; 001 и 110; 010 и 101; 011 и 100.
В общем виде два противоположных набора записываются в виде (x1, x2, ..., xn) и (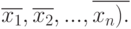
Переключательная функция n переменных f* (x1, x2, ..., xn) называется двойственной к функции f(x1, x2, ..., xn) , если имеет место равенство:

Например, для функции дизъюнкции f (x1, x2) = x1 v x2 двойственной будет функция конъюнкции f* (x1, x2) = x1 & x2.
Переключательная функция называется самодвойственной, если на каждой паре противоположных наборов она принимает противоположные значения, т. е. если выполняется условие:
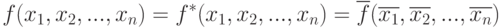
Пример самодвойственной функции: F(x1,x2,x3) = ?(1,2,3,7)
| Набор | x1 | x2 | x3 | F(x1,x2,x3) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 1 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 |
При определении свойства монотонности переключательной функции используется понятие сравнимости двух наборов аргументов.
Примем условие, что 0 < 1 (на самом деле, для логической функции корректнее было бы писать: false < true, но это смотрится у совсем несерьезно и в свете дальнейших рассуждений оставим все-таки исходный вариант). Два набора аргументов X = (x1, x2, ..., xn) и Z = ( z1, z2, ..., zn ) называются сравнимыми, если для всех аргументов выполняется условие xi =< zi (говорят, что X =< Z). Иными словами, если значение каждого аргумента одного набора меньше или равно значению того же аргумента второго набора, то говорят, что первый набор меньше или равен второму (не больше второго). И наоборот. Если значение каждого аргумента одного набора больше или равно значению того же аргумента второго набора, то говорят, что первый набор больше или равен второму (не меньше второго).
Например, если X = (0000) и Z = (0001), то наборы сравнимы, и X < Z.
Если же некоторые из значений аргументов первого набора больше или равны, а другие меньше значений тех же аргументов второго набора, то такие наборы называются несравнимыми.
Например, если X = (1010) и Z = (0110), то эти наборы являются несравнимыми (x1 > z1, но x2 < z2).
Переключательная функция называется монотонной, если для всех пар сравнимых наборов при любом возрастании набора значение этой функции не убывает, т.е. сохраняет свое значение или изменяется с 0 на 1. Здесь, аналогично обычной математике, можно рассматривать монотонно возрастающие и монотонно убывающие функции, но для наших дальнейших рассуждений это не будет иметь какого-либо значения.
Т.е. для монотонной логической функции должно выполняться условие: если для сравнимых наборов X =< Z , то F(X) =< F(Z).
Примеры: монотонная функция: F1(x1, x2) = x2,
Для упрощения анализа данной таблицы отметим, что наборы (0,1) и (1,0) являются несравнимыми. Поэтому значения функции для определения ее монотонности на этих наборах делать не следует.
Переключательная функция называется линейной, если она может быть представлена полиномом Жегалкина11Иван Иванович Жегалкин (1869 - 1947) — российский и советский математик и логик. первой степени (каждая конъюнкция содержит только одну переменную), т.е. записана в виде:
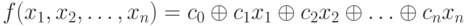 , где
, где

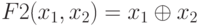
 – символ
– символ