| Россия, г. Москва |
Функционально-полные системы логических функций. Свойства логических функций
Выделение всех функционально полных наборов ФАЛ даже для функций двух переменных с относительно небольшим количеством функций является весьма трудоемкой задачей, которая может решаться либо перебором, либо какими-то эвристическими методами. А для функций от трёх переменных (общее количество таких функций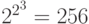 ) это становится непосильной задачей.
) это становится непосильной задачей.
На практике используются несколько наиболее известных таких наборов:
F1 = {&, V , ? } – "И, ИЛИ, НЕ"
F2 = {/} – "штрих Шеффера"
F4 = {"Сумма по mod2", "И", "Константа 1"} – "базис Жегалкина".
Как видим из Табл. 4.1, все они удовлетворяют теореме Поста – Яблонского, поэтому являются функционально полными.
На первом этапе вопрос ставится так, чтобы в функционально полный набор функций входило их ограниченное количество.
Уже на примере анализа функций, входящих в набор F1, можно сделать вывод, что данный набор является избыточным: удаление из него функции "И" или функции "ИЛИ" всё равно приводит к тому, что остающиеся две функции удовлетворяют требованиям теоремы Поста – Яблонского, а, следовательно, наборы из функций {"И", "НЕ"} и {"ИЛИ", "НЕ"} тоже функционально полны. Из этих наборов ни одну функцию убрать уже нельзя без того, чтобы они не перестали быть функционально полными.
В то же время наборы F2 и F3 состоят всего лишь из одной функции. Поэтому нет смысла их каким-либо образом сокращать.
В связи с этим помимо понятия "функционально полный набор логических функций" используется также понятие "логический базис".
Второй этап призван дать ответ на вопрос: "Все ли ФАЛ входящие в эти или какие-либо другие наборы являются необходимыми для обеспечения функциональной полноты набора?".
Система функций F={f1, f2,…,fn} называется базисом, если она полна, но всякая её собственная подсистема не является полной.
Дать ответ на вопрос о включении той или иной функции в состав функционально полного набора, а тем более, базиса не представляется возможным. Можно дать лишь верхнее ограничение на количество логических функций, входящих в базис, на основе следующей теоремы.
Теорема Яблонского
Из всякой полной системы логических функций можно выделить полную подсистему, содержащую не более четырех логических функций.
Таким образом, любой базис логических функций содержит не более четырех ФАЛ.
Краткие итоги
В лекции дано определение полноты системы логических функций. Описаны основные свойства ФАЛ. На основании свойств логических функций от двух переменных согласно теореме Поста-Яблонского представлены примеры наиболее часто используемых в вычислительной технике функционально-полных наборов логических функций. Определено понятие базиса логических функций.
Контрольные вопросы
- Какими свойствами обладает функционально полная система логических функций?
- Пусть задана функционально полная система логических функций
- F= {f1,f2,...,fn}. В каком случае система логических функций G={g1,g2,...,gm} также будет функционально полной?
- Назовите основные свойства логических функций.
- Какая логическая функция называется сохраняющей ноль?
- Какие из следующих логических функций двух переменных являются сохраняющими ноль: конъюнкция, дизъюнкция, сумма по модулю два, штрих Шеффера, стрелка Пирса? Почему?
- Какая логическая функция называется монотонной сохраняющей единицу?
- Какие из следующих логических функций двух переменных являются сохраняющими единицу: конъюнкция, дизъюнкция, сумма по модулю два, штрих Шеффера, стрелка Пирса? Почему?
- Какая логическая функция называется монотонной?
- Какие из указанных наборов являются сравнимыми (несравнимыми): X= 0110 и Z = 0010, x = 1100 и Z = 1000? Почему?
- Какие из следующих логических функций двух переменных являются монотонными: конъюнкция, дизъюнкция, сумма по модулю два, штрих Шеффера, стрелка Пирса? Почему?
- Какая логическая функция линейной?
- Какая логическая функция называется самодвойственной?
- В каком случае логическая функция g(x1,x2,...,xn) называется двойственной логической функции f(x1,x2,...,xn)?
- Какие из следующих логических функций являются самодвойственными: конъюнкция, дизъюнкция, сумма по модулю два, штрих Шеффера, стрелка Пирса? Почему?
- Какими свойствами обладает система логических функций, составляющих базис?
- Какова максимальная мощность множества логических функций, составляющих базис?
