Функционально-полные системы логических функций. Свойства логических функций

Теорема Поста – Яблонского о функциональной полноте системы логических функций

Для того чтобы система переключательных функций была функционально полной, необходимо и достаточно, чтобы эта система включала:

• хотя бы одну переключательную функцию, не сохраняющую нуль;
• хотя бы одну переключательную функцию, не сохраняющую единицу;
• хотя бы одну несамодвойственную переключательную функцию;
• хотя бы одну немонотонную переключательную функцию;
• хотя бы одну нелинейную переключательную функцию.

Рассмотрим все функции от двух переменных f(x₀, x₁) с точки зрения удовлетворения ими рассмотренным выше свойствам (Табл. 4.1).

Таблица 4.1.

Свойства функций двух переменных
Функция	Сохранение "0"	Сохранение "1"	Самодвойственная	Монотонная	Линейная
	+			+	+
	+
			+		+
	+
			+		+
	+				+
	+	+		+
		+			+
	+	+	+	+	+
		+
	+	+	+	+	+
		+
	+	+		+
		+		+	+

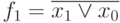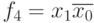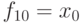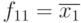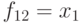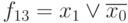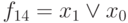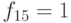Мы видим, что как, собственно, и следовало ожидать, если включить в состав функционально полного набора все функции от данного числа переменных, то с его помощью мы, даже не прибегая к суперпозиции каких-либо функций, сможем выразить любую ФАЛ.