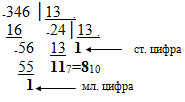| Россия, г. Москва |
Системы счисления. Перевод чисел из одной системы счисления в другую
Перевод целых чисел
Метод 1. Данный метод используется наиболее часто. Его суть состоит в том, что исходное p-ичное число делится на основание q новой системы счисления. Получаемый остаток представляет собой p-ичную запись q-ичной цифры нового представления числа. Частное от деления вновь делится на основание qновое системы счисленияи т.д. до тех пор, пока не будет получено частное, меньшее, чем q. Запись нового представления числа начинается с младшей цифры. Действия производятся в p-ичной системе счисления.
Обоснование метода 1:
Ap = an*pn+an-1*pn-1+…+a1*p1+a0*p0
Bq = br*qr+br-1*qr-1+…+b1*q1+b0*q0
Aq /q = {А1,S1}, гдеА1 –целая часть результата, S1 – остаток.
Bq /q = {В1,R1}, гдеB1- целая часть результата, R1-остаток.
B1= br*qr-1+br-1*qr-2+…+b1*q0
R1= b0
Т.к. Ap ? Bq,тоb0 = S1.
Пример 6.1. Перевести число 179 из 10-й системы счисления в 7-ю.
В результате преобразования получим: 18110= 3467
Пример 6.2. Перевести число 346 из 7-й системы счисления в 10-ю.
При выполнении этого перевода необходимо помнить следующие особенности:
- действия проводятся в исходной системе счисления и, следовательно, основание новой системы счисления тоже должно быть представлено в исходной системе счисления;
- т.к. при переводе числа в систему счисления с бОльшим основанием остаток может получиться многозначным числом, которое при представлении исходного числа в новой системе счисления должен быть представлен одной цифрой в новой системе счисления.
Так, 35 х 35 = 215, т.к. символа "6" в 5-й системе счисления нет, а согласно общей записи числа в позиционной системе счисления (см 6.1) 215 = 2*51 + 1*50.
Основание новой системы счисления будет представлено в исходной 7-й системе значением: 1010 = 137.
Вернемся к нашему первому методу перевода. Выполним перевод:
На одном из этапов деления мы получили остаток, меньший делителя, но не являющийся одной цифрой. Вспомним, что мы переводим число в систему счисления с бОльшим основанием, где количество символов для представления знаков числа больше, поэтому запишем окончательный результат:
3467 = 18110,
что согласуется с предыдущим примером.
Метод 2. Все цифры и основание представления числа согласно формуле (6.1) в исходной системе счисления записываются в новой системе счисления. Над полученным выражением проводятся вычисления, результат которых и будет представлять собой запись исходного числа в новой системе счисления.
Пример. Перевести число 321 из 4-й в 3-ю систему счисления.
3214 = (3х42+2х41+1х40)4 = (10х112+2х111+1х110)3 =
= (10х11х11+2х11+1)3 = 20103
3214 = 20103