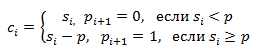| Россия, г. Москва |
Системы счисления. Перевод чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую
При переводе чисел из одной позиционной системы счисления в другую необходимо выполнять различные арифметические операции. Не останавливаясь подробно на механизме выполнения этих операций в каждой системе счисления, отметим лишь, что числа, представленные в различных позиционных системах счисления, обрабатываются схожим образом с учётом, естественно, особенностей данной системы счисления и имеющихся в ней символов.
Так, на примере операции сложения это будет выглядеть следующим образом:
Cq = Aq +Bq
Aq = an*qn+an-1*qn-1+…+a1*q1+a0*q0
Bq = bm*qm+bm-1*qm-1+…+b1*q1+b0*q0
Промежуточная сумма:
si = ai+bi+ pi-1 ,
где ai, и bi - соответствующие разряды слагаемых,
pi-1– перенос из предыдущего разряда.
Пример:
52648 + 65318 = 140158
Выполнение операции по шагам:
| +5 | 2 | 6 | 4 | A8 | |
| 6 | 5 | 3 | 1 | B8 | |
| 11 | 7 | 9 | 5 | S1 | |
| +3 | 7 | 1 | 5 | C1 | |
| 1 | 0 | 1 | 0 | 0 | P1 |
| 1 | 3 | 8 | 1 | 5 | S2 |
| 1 | 3 | 0 | 1 | 5 | C2 |
| 0 | 1 | 0 | 0 | 0 | P2 |
| 1 | 4 | 0 | 1 |
58 |
S3=A+B |
Для перевода смешанного числа, то есть числа, содержащего как целую, так и дробную части, из p-ичной системы счисления в q-ю существует несколько способов.
Прежде всего, отметим, что перевод целой части числа и его дробной части осуществляется по различным правилам. Рассмотрим некоторые из них.