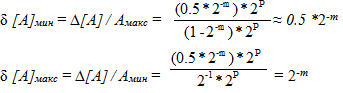| Россия, г. Москва |
Системы счисления. Перевод чисел из одной системы счисления в другую
Погрешности представления чисел
Абсолютная погрешность представления – разность между истинным значением входной величины А и ее значением, полученным из машинного изображения Ам, т. е.
?[А] = А –Ам. ,
где Ам – машинное представление величины А, которое отличается от истинной в силу ограниченного количества разрядов машинной сетки.
Относительная погрешность представления – величина
? [А] = ?[А] / А
Погрешности представления чисел с фиксированной точкой
Абсолютная погрешность составляет половину единицы младшего разряда числа.
Для правильных дробей (числа с фиксированной запятой):
?[А] = 0.5* 2-n.
? [А]мин = ?[А] / Амакс = (0.5 * 2-n)/ (1-2-n) ? 0.5 *2-n
? [А]макс = ?[А] / Амин = (0.5 * 2-n) / 2-n = 0.5
Для целых чисел (числа с фиксированной точкой):
?[А] = 0.5* 20= 0.5.
? [А]мин = ?[А] / Амакс = 0.5 / (2п-1) ?0.5 / 2п =0.5* 2-n
? [А]макс = ?[А] / Амин = 0.5 / 1 = 0.5
Как мы видим, и в том и в другом случае эта погрешность может существенно меняться в зависимости от представляемой величины.
Диапазон и точность представления чисел с плавающей запятой
k – порядок числа;
M – мантисса числа
Пример:
567 = 567*100 = 5670*10-1 = 5,67*102 = 0,567*103 = 0,00567*105 = …
Нормализованная мантисса удовлетворяет условию:
1 > |M| ? p-1
567 ? 0,567*103
|
ЗнП |
2n-1 |
. . . |
21 |
20 |
ЗнМ |
2-1 |
2-2 |
. . . |
2-m |
| Порядок (n+1 разряд) | Мантисса (m+1разряд) | ||||||||
Пмакс = 0,1 ... 1 = 2п-1
М макс = 0,1 ... 1 = 1-2-m
-Пмакс = -(2п-1)
М мин = 0,1 = 2-1
Погрешности представления чисел с плавающей запятой
?[А] = 0.5* 2-m* 2P
? [А]мин = ?[А] / Амакс = ((0.5 * 2-m) * 2P) /((1-2-m) * 2P)? 0.5 *2-m
? [А]макс = ?[А] / Амин = ((0.5 * 2-m) * 2P) / 2-1 = 2-m
Особенности использования действующего в настоящее время ГОСТа 754-2008 на представление чисел с плавающей запятой мы обсудим в лекции, касающейся порядка обработки таких чисел и особых ситуаций, встречающихся в процессе этой обработки.
Краткие итоги
Рассмотрены типы систем счисления. По критерию минимальности используемого оборудования выбрана двоичная система счисления для реализации элементов вычислительной техники. Приведены правила перевода целых и дробных чисел из одной произвольной системы счисления в другую. Особое внимание обращено на перевод чисел, представленных в 2k-ичных системах счисления (двоичных, восьмеричных, 16-ных) между собой, что, с одной стороны, выполняется достаточно просто, а с другой стороны, требуется делать относительно часто в тех или иных случаях как при программировании, так и при разработке аппаратуры. Показаны механизмы расчета диапазонов представления и погрешностей для чисел различных форматов.
Контрольные вопросы
- Чем отличаются позиционные системы счисления от непозиционных? Приведите примеры позиционных и непозиционных систем счисления.
- Укажите достоинства, недостатки и области применения позиционных и непозиционных систем счисления.
- Запишите число "14" в римской системе счисления.
- Запишите число "5" 3-й и 9-й системах счисления.
- Укажите методы перевода целых чисел из одной позиционной системы счисления в другую.
- Переведите число 5323 из 7-й системы счисления в 5-ю и 9-ю различными методами. Сравните полученные результаты. Если результаты не совпадают, объясните причину расхождения.
- В какой системе счисления одно и то же число буде иметь больше знаков: в системе с бОльшим или с меньшим основанием? Почему? Всегда ли число в системах с разными основаниями имеет разное количество знаков?
- Одно и то же число записано в системах счисления с разными основаниями. Можно ли сказать, для какой записи числа основание системы счисления больше?
- Укажите методы перевода правильных дробей из одной позиционной системы счисления в другую.
- Всегда ли правильная конечная дробь в одной системе счисления будет правильной конечной дробью в другой системе счисления? Почему?
- Как определяется количество разрядов, которое необходимо для представления правильной конечной дроби в другой системе счисления? Каким образом определяется соотношение между количеством разрядов правильной дроби в разных системах счисления?
- Как производится округление дробной части числа в p-й системе счисления?
- В какой системе счисления для указания дробной части числа потребуется большее количество разрядов: в системе счисления с бОльшим или с меньшим основанием? Почему?
- Укажите методы перевода смешанных чисел из одной позиционной системы счисления в другую.
- Переведите число 345, 67 из 8-й системы счисления в 5-ю и 9-ю.
- Как определяется диапазон представления двоичных чисел с фиксированной точкой?
- Как определяется диапазон представления двоичных чисел с фиксированной запятой?
- Как определяется диапазон представления двоичных чисел с плавающей запятой?
- Как определяется относительная погрешность представления двоичных чисел с фиксированной точкой?
- Как определяется относительная погрешность представления двоичных чисел с фиксированной запятой?
- Как определяется относительная погрешность представления двоичных чисел с плавающей запятой?
- Укажите достоинства и недостатки представления двоичных чисел в виде чисел с фиксированной точкой, фиксированной запятой, плавающей запятой.
- Какие характеристики числа с плавающей запятой изменятся при изменении количества разрядов, отводимых под порядок и под мантиссу числа?
- Для двоичного числа, представленного в формате с плавающей запятой, 3 разряда отведено под порядок и 7 разрядов – под мантиссу (знаки не учитываются). Укажите диапазон изменения таких чисел, максимальную и минимальную погрешности.