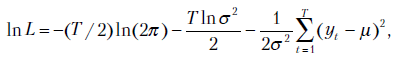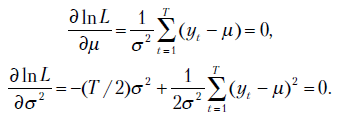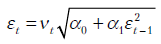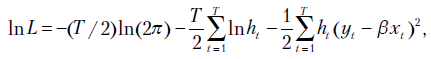|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Инспектор
Вы можете этот курс.
Опубликован: 10.09.2016 | Уровень: для всех | Доступ: платный
Лекция 11:
Временные ряды с высокой изменчивостью
11.4. ММП-оценка моделей ОАРУГ и АРУГ-М
Рассмотрим метод максимума правдоподобия, необходимый для понимания и написания программ для АРУГ-моделей.
Предположим, что значения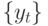 
-последовательности нормально распределены со средним 
и постоянной дисперсией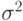 
. Из теории вероятностей следует, что логарифм функции правдоподобия, использующей
независимых наблюдений, распределенных по нормальному закону, имеет вид
Задача состоит в максимизации функции правдоподобия по неизвестным параметрам и 
по известным выборочным данным 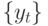. Приравняв к нулю частные производные первого порядка, имеем:
Решая систему уравнений относительно и , получаем:
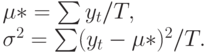
Те же принципы применяются и в регрессионном анализе.
Предположим, что последовательность 
получена из модели
В классической регрессионной модели предполагается, что среднее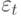 
равно нулю, дисперсия равна 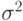и различные реализации независимы и подчинены нормальному распределению вероятностей. Тогда функция правдоподобия принимает вид
Максимизируя по 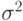и, получаем стандартные формулы МНК для коэффициентов регрессии
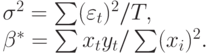
До сих пор мы получали линейные относительно неизвестных условия первого порядка. К сожалению, для АРУГ-моделей условия первого порядка оказываются нелинейными, и их решение требует более сложных алгоритмов.
Рассмотрим, к примеру, АРУГ(1)-процесс для ошибок регрессионной модели. Снова будем исходить из того, что 
, но условная дисперсия 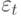представима в виде
и потому равна
Хотя условная дисперсия 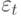не постоянна, легко ввести необходимые поправки в функцию правдоподобия
где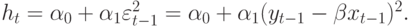 
Следует максимизировать функцию относительно 
и 
. Многие компьютерные программы позволяют провести такую максимизацию итерационными методами.
Контрольные вопросы
- Чем была вызвана необходимость исследования моделей с условной гетероскедастичностью?
- Что собой представляют АРУГ-модели, какому процессу подчиняется в этих моделях условная дисперсия ошибки исходного временного ряда?
- Покажите, что прогнозы для
-модели (11.16) имеют вид авторегрессии порядка 
, т.е. являются процессами вида
- Дайте определение ОАРУГ-модели. Каковы отличия в поведении условной дисперсии остатков АРУГ- и ОАРУГ-моделей?
- Какова область применения моделей АРУГ-М, чем они отличаются от АРУГ-моделей?
- Опишите метод максимального правдоподобия для оценок коэффициентов АРУГ-модели Энгла (11.4, 11.11).
