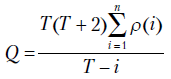НОУ ИНТУИТ | Введение в эконометрику. Лекция 11: Временные ряды с высокой изменчивостью

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 10.09.2016 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 27 студентам

| Поделиться |

Поддержать программу

11.2. Обобщенные авторегрессионные условно гетероскедастические модели (ОАРУГ-модели)

В 1986 г. Т. Болеслев обобщил работу Р. Энгла, предположив, что условная дисперсия может представлять АРСС-процесс. В этом случае ошибки наблюдений описываются формулой

$\varepsilon _{t} = \nu _{t} \sqrt{ht},$

(11.17)

где и

(11.18)

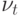Так как $\nu _{t}$ - белый шум, не зависящий от прошлых реализаций 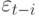$\varepsilon _{t-i}$ , то условные и безусловные средние $\varepsilon _{t }$ равны нулю. Важным моментом является формула условной дисперсии для $\varepsilon _{t }$

(11.19)

Обобщенная АРУГ(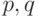 p, q )-модель (ОАРУГ-модель) позволяет ввести авторегрессионные компоненты и слагаемые типа скользящего среднего в гетероскедастическую дисперсию.

Выгода от применения ОАРУГ-моделей очевидна. Кроме того, использование этих моделей позволяет придать более экономный и простой вид описанию модели. Такие модели содержат меньше коэффициентов для оценки, а значит, меньше ограничений на эти коэффициенты.

Ключевым моментом в ОАРУГ-моделях является тот факт, что возмущения 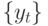$\{y_{t}\}$ -последовательности образуют АРСС-процесс. Допустим, необходимо оценить 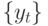$\{y_{t}\}$ -последовательность с помощью некоторой АРСС-модели. Если модель адекватна, то АКФ и ЧАКФ остатков будут указывать на белый шум. Однако АКФ квадратов остатков могут помочь идентифицировать порядок ОАРУГ-процесса. Исходя из того, что $M_{t-1}\varepsilon _{t }^{2}- h_{t}$ перепишем (11.18) в виде

(11.20)

Уравнение (11.20) представляет АРСС-процесс для $\{\varepsilon _{t}^{2}\}$ -последовательности. Если в процессе присутствует условная гетероскедастичность, то коррелограмма квадратов остатков будет удовлетворять условиям именно такой модели. Последовательность построения коррелограммы следующая.

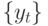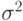Сначала оцениваем $\{y_{t}\}$ -последовательность с помощью лучшей из АРСС-моделей (как это описано в главе 10). Находим $\varepsilon _{t}^{2}$ -квадраты ошибок модели. Вычисляем выборочную дисперсию остатков $\sigma ^{2}$ по формуле

где

-

число остатков.

Вычисляем и графически изображаем выборочные автокорреляции квадратов остатков по формуле

Для больших выборок стандартное отклонение $\rho (i)$ может быть взято приблизительно равным $Т^{-1/2}$ . Если значение $\rho (i)$ сильно отличается от нуля, то это свидетельствует о наличии ОАРУГ-процесса.

Как и в главе 10, -статистика

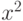имеет $x^{2}$ -распределение с n степенями свободы, если $\varepsilon _{t}^{2}$ не коррелированы. Если эта гипотеза отвергается, значит, необходимо принять ОАРУГ-модель. На практике обычно полагают n = T/4 .

Более строгий тест, использующий мультипликатор Лагранжа, для обнаружения существования АРУГ-процесса предложил P. Энгл (1982). Его методология включает два шага:

МНК-оценку наиболее подходящей АР(n)-модели $y_{t }= a_{0} + a_{1}y_{t-1} + a_{2}y_{t-2} + \dots + a_{n}y_{t-n} + \varepsilon _{t } ;$
вычисление квадратов ошибок модели $\varepsilon _{t}^{2}$ . Строим авторегрессию порядка квадратов остатков

(11.21)

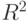Если не подходит ни одна из АРУГ-моделей, то все $\alpha _{i} (i = 1, \dots , q)$ равны нулю и $R^{2}$ -статистика будет мала. Статистика $ТR^{2}$ будет сходиться к $x^{2}_{q}$ - распределению. Если $ТR^{2 }$ больше критического значения $x^{2}_{q}$ - распределения при заданном уровне значимости, то это свидетельствует о необходимости принять АРУГ-гипотезу.
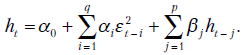
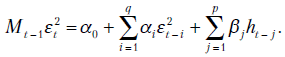
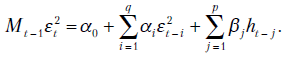
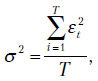