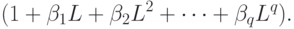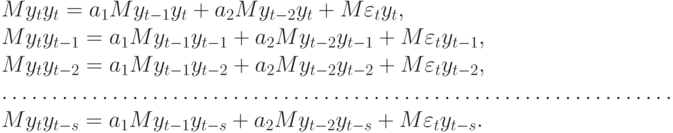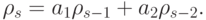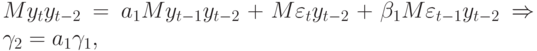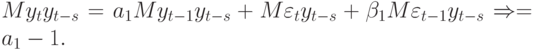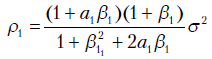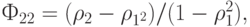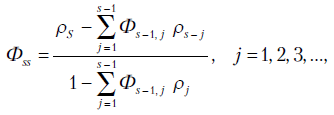|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Стационарные временные ряды, модели авторегрессии - скользящего среднего
10.5. Автокорреляционные функции (АКФ)
Автоковариации и автокорреляции (см. (10.12) и (10.13)) весьма полезны при построении АРСС(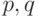 )-моделей. Проиллюстрируем метод автокорреляционных функций на четырех важных примерах, встречающихся примерно в 80% приложений: моделях АР(1), АР(2), СС(1), АРСС(1, 1).
)-моделей. Проиллюстрируем метод автокорреляционных функций на четырех важных примерах, встречающихся примерно в 80% приложений: моделях АР(1), АР(2), СС(1), АРСС(1, 1).
АКФ для АР(1)-модели 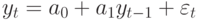 формулы (10.13), (10.19) дают:
формулы (10.13), (10.19) дают:
![\gamma_{t} = \sigma ^{2}/[1 - (a_{1})^{2}],\\
\gamma_{s} = \sigma ^{2}(a_{1})^{s}/[1 - (a_{1})^{2}].](/sites/default/files/tex_cache/c382181dab4a7d6ab85d5ced284376b8.png)
Из (10.13) получаем, что  .
.
Построим график, на оси абсцисс отложив значение  , а на оси ординат -
, а на оси ординат - 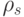 . Напомним, что такой график называется коррелограммой. В нашем случае автокорреляционные функции
. Напомним, что такой график называется коррелограммой. В нашем случае автокорреляционные функции 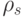 сходятся к нулю со скоростью геометрической прогрессии (
сходятся к нулю со скоростью геометрической прогрессии ( по условию). Если
по условию). Если , то сходимость монотонно убывающая. При
, то сходимость монотонно убывающая. При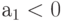 наблюдаются колебания, амплитуда которых затухает со скоростью геометрической прогрессии.
наблюдаются колебания, амплитуда которых затухает со скоростью геометрической прогрессии.
АКФ для АР(2)-модели. АР(2)-процесс более сложный:
Мы опустили свободный член, поскольку он не оказывает влияния на величину АКФ. Напомним, что по условиям стационарности корни характеристического многочлена  лежат вне единичного круга. Выведем расчетные формулы для автокорреляций, используя уравнения Юла - Уокера.
лежат вне единичного круга. Выведем расчетные формулы для автокорреляций, используя уравнения Юла - Уокера.
Умножим уравнение (10.27) на 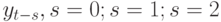 и т.д. После вычисления математического ожидания в левой и правой частях равенств получаем систему уравнений
и т.д. После вычисления математического ожидания в левой и правой частях равенств получаем систему уравнений
Согласно определению стационарности,
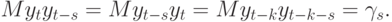
Далее ясно, что
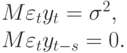
Поэтому (10.28) преобразуется к следующему виду:

Поделив (10.30) и (10.31) на 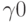 , получаем:
, получаем:

Поскольку 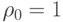 , из (10.32) следует, что
, из (10.32) следует, что 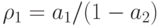 . Зная
. Зная 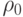 и
и 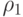 , далее последовательно находим остальные АКФ. Например, для
, далее последовательно находим остальные АКФ. Например, для 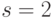 и
и  имеем
имеем
![r_{2} = (a_{1})^{2}/(1 - a_{2})+ a_{2},\\
r_{3} = a_{1}[(a_{1})^{2}/(1 - a_{2})+ a_{2}] + a_{2}a_{1}/(1 - a_{2}).](/sites/default/files/tex_cache/80a480c9252f42c4698954a74d51878d.png)
Как и в предыдущем случае, последовательность АКФ  должна быть сходящейся. Согласно условиям стационарности
должна быть сходящейся. Согласно условиям стационарности  корни характеристического уравнения для разностного уравнения (10.33) должны лежать внутри единичного круга.
корни характеристического уравнения для разностного уравнения (10.33) должны лежать внутри единичного круга.
АКФ для СС(1)-модели. Рассмотрим СС(1)-процесс вида 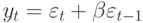 . Умножая
. Умножая  на
на 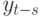 и вычисляя математическое ожидание, получаем уравнения Юла - Уокера
и вычисляя математическое ожидание, получаем уравнения Юла - Уокера
![\gamma_{1} = D(y_{t}) = My_{t}y_{t} = M[(\varepsilon _{t} + \beta \varepsilon _{t-1})(\varepsilon _{t} + \beta \varepsilon _{t-1})] = (1+\beta ^{2}) \sigma ^{2},\\
\gamma_{1} = My_{t}y_{t-1} = M[(\varepsilon _{t} + \beta \varepsilon _{t-1})(\varepsilon _{t-1} + \beta \varepsilon _{t-2})] = \beta \sigma ^{2}](/sites/default/files/tex_cache/7d2fa7493c22f7f2787f9b471a7032fa.png)
и
![\gamma_{s} = My_{t}y_{t-s} = M[(\varepsilon _{t} + \beta \varepsilon _{t-1})(\varepsilon _{t-s} + \beta \varepsilon _{t-s-2})] = 0 для s > 1.](/sites/default/files/tex_cache/3c771b7075f5b2db93b880be68382ba1.png)
АКФ для АРСС(1, 1)-модели. Пусть

Используя прием Юла - Уокера, получаем

Из (10.34) и (10.35) имеем:
Следовательно,
и далее 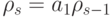 для
для 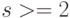 .
.
Итак, в АРСС(1, 1)-модели величина 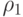 зависит от
зависит от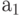 и
и 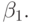 Далее
Далее 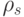 АРСС(1, 1) выглядит так же, как для АР(1), т.е. имеет вид последовательности членов геометрической прогрессии со знаменателем
АРСС(1, 1) выглядит так же, как для АР(1), т.е. имеет вид последовательности членов геометрической прогрессии со знаменателем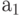 . В зависимости от знака
. В зависимости от знака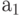 эта последовательность либо постоянно убывает, либо осцилирует, затухая.
эта последовательность либо постоянно убывает, либо осцилирует, затухая.
Частные автокорреляционные функции (ЧАКФ). В АР(1)-модели  и
и 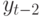 коррелируют, хотя
коррелируют, хотя 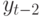 явно не входит в уравнение модели
явно не входит в уравнение модели 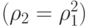 . Такая косвенная корреляция присуща АКФ любой авторегрессионной модели. Частные автокорреляции между
. Такая косвенная корреляция присуща АКФ любой авторегрессионной модели. Частные автокорреляции между  и
и 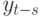 , напротив, исключают эффекты других запаздываний. Поэтому для АР(1)-модели ЧАКФ между
, напротив, исключают эффекты других запаздываний. Поэтому для АР(1)-модели ЧАКФ между  и
и 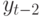 равны нулю.
равны нулю.
Большинство статистических пакетов программ имеют возможности для вычисления ЧАКФ. Некоторые из них основаны на методе, связанном с уравнениями Юла - Уокера,
и далее
где
Используя правило Крамера, из уравнений Юла - Уокера можно для АP( )-процесса получить другую формулу для Фkk:
)-процесса получить другую формулу для Фkk:
Для  , прямой корреляции между
, прямой корреляции между  и
и 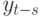 для АР(
для АР( )-процесса нет. Следовательно,
)-процесса нет. Следовательно,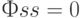 при
при  .
.
Рассмотрим теперь СС(1)-модель 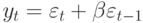 . Если
. Если 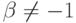 , то
, то 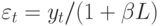 . Следовательно, разлагая правую часть равенства в ряд, имеем:
. Следовательно, разлагая правую часть равенства в ряд, имеем:

Поэтому ЧАКФ для СС(1) не обращаются в ноль, начиная с некоторого номера  , а убывают со скоростью геометрической прогрессии. Если
, а убывают со скоростью геометрической прогрессии. Если  , то убывание монотонное, а при
, то убывание монотонное, а при  коэффициенты осцилируют. В более общем случае ЧАКФ стационарных АРСС(
коэффициенты осцилируют. В более общем случае ЧАКФ стационарных АРСС(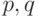 )-процессов, начиная с лага
)-процессов, начиная с лага  , убывают к нулю. Вид убывания зависит от коэффициентов многочлена:
, убывают к нулю. Вид убывания зависит от коэффициентов многочлена: