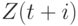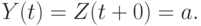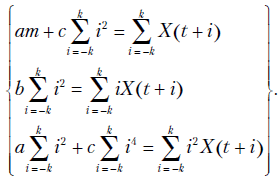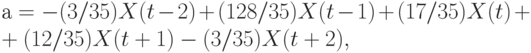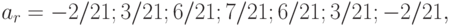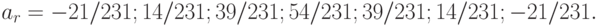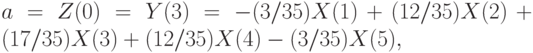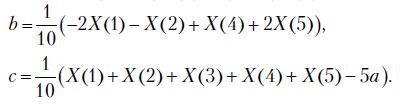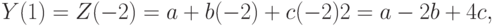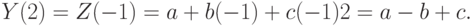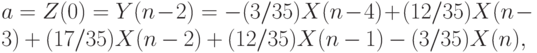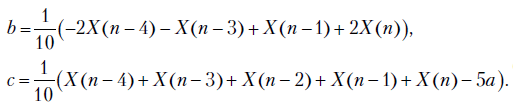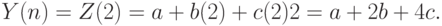|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Сглаживание временных рядов
6.3. Методы взвешенных скользящих средних
Суть методов взвешенных скользящих средних заключается в том, что значениям исходного ряда приписывается вес  , зависящий от расстояния до середины интервала сглаживания, т.е. от
, зависящий от расстояния до середины интервала сглаживания, т.е. от 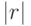 . Тогда
. Тогда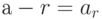 и сглаживание по этим методам является центрированным и симметричным. Для определения весов прибегают к различным подходам.
и сглаживание по этим методам является центрированным и симметричным. Для определения весов прибегают к различным подходам.
Рассмотрим первый подход. Пусть весами являются члены разложения бинома (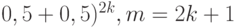 . Тогда
. Тогда
При этом 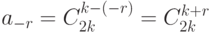 . По свойству сочетаний имеем
. По свойству сочетаний имеем
Получаем:
при 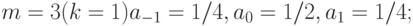
при 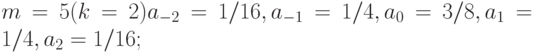
при 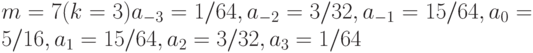 .
.
Второй подход заключается в подборе полинома регрессии к данным, содержащимся в интервале сглаживания. При этом свободный член а полинома регрессии выбирается равным расчетному значению ряда  .
.
Рассмотрим случай, когда уравнение регрессии квадратичное, т.е. сглаживание происходит на основе уравнения параболы. В этом случае для каждого набора m последовательных членов исходного ряда составляется система 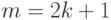 уравнений для расчета по методу наименьших квадратов:
уравнений для расчета по методу наименьших квадратов:
Сглаженное значение ряда  выбирается по формуле
выбирается по формуле
Запишем систему нормальных уравнений для определения коэффициентов параболы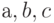
Так как 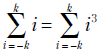 получаем из системы (6.7)
получаем из системы (6.7)
Исключив из первого и третьего уравнений системы (6.8), получаем формулу для расчета коэффициента
из первого и третьего уравнений системы (6.8), получаем формулу для расчета коэффициента
При 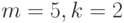 имеем
имеем
т.е.  .
.
Аналогично для 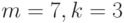 и для
и для 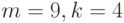 соответственно получаем
соответственно получаем
Можно легко проверить, что если в качестве сглаживающего многочлена взять прямую, то коэффициенты  , т.е. совпадут с коэффициентами сглаживания с помощью метода простой скользящей средней.
, т.е. совпадут с коэффициентами сглаживания с помощью метода простой скользящей средней.
Предположим, дисперсия уровней исходного ряда постоянная и равна 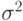 , а сами члены ряда
, а сами члены ряда 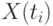 независимы между собой. В этом случае дисперсия сглаженного по квадратичному полиному ряда
независимы между собой. В этом случае дисперсия сглаженного по квадратичному полиному ряда  равна
равна
При 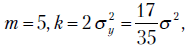 а при
а при 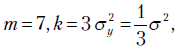 т.е. тенденция к уменьшению дисперсии с ростом m сохраняется.
т.е. тенденция к уменьшению дисперсии с ростом m сохраняется.
При сглаживании с помощью скользящей средней нет возможности получить сглаженные значения для  первых и
первых и  последних членов ряда
последних членов ряда 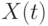 . В случае сглаживания с помощью полинома регрессии для крайних членов исходного ряда могут быть получены сглаженные значения - значения полинома регрессии в этих точках. Но для этого надо оценить не только свободный член a полинома, но и остальные коэффициенты полинома регрессии (коэффициенты
. В случае сглаживания с помощью полинома регрессии для крайних членов исходного ряда могут быть получены сглаженные значения - значения полинома регрессии в этих точках. Но для этого надо оценить не только свободный член a полинома, но и остальные коэффициенты полинома регрессии (коэффициенты  , с в квадратичном случае). Из системы (6.8) получаем
, с в квадратичном случае). Из системы (6.8) получаем
Для 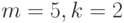 из (6.10), (6.13) для начальных значений ряда имеем
из (6.10), (6.13) для начальных значений ряда имеем
Для последних пяти членов ряда аналогично получаем ( - объем выборки):
- объем выборки):

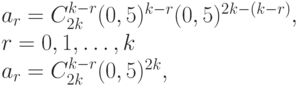
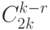
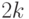 элементов по
элементов по  элементов.
элементов.