Инструменты Gnumeric для статистиков
5.11 Два средних
Вложенное меню "Два средних" ("Статистика/Тесты с двумя выборками/Два средних") предоставляет набор инструментов для проверки гипотезы о равенстве (или неравенстве) средних значений выборок (генеральных совокупностей). В качестве исходных данных будем средствами Gnumeric генерировать выборки с нормальным распределением.
5.11.1 Равные выборки: T-тест
Пусть известно, что в двух выборках имеется равное количество значений случайных величин, и известно, что у этих выборок равные дисперсии. В данном случае T-тест дает возможность определить дисперсии и средние значения для этих выборок и посчитать разницу между средними.
Для примера рассмотрим 25 нормально распределенных случайных значений со средним значением 5 и стандартным отклонением 1 (Выборка1) и 25 нормально распределенных случайных значений со средним значением 7 и стандартным отклонением 1 (Выборка2).
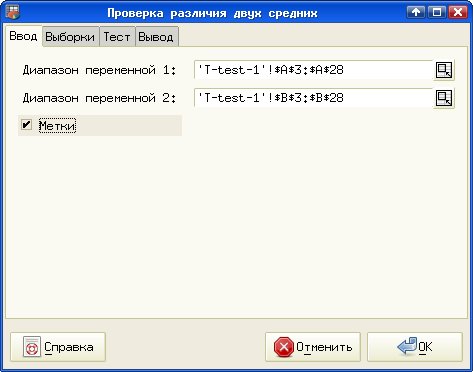
На вкладке "Ввод" диалога "Проверка различия двух средних" ("Статистика/Тесты с двумя выборками/Два средних/Равные выборки: T-тест...") указываем диапазоны для исходных данных, причем нужно проследить, чтобы все адреса были абсолютными (см. рис. 5.36). Режим "Метки", как всегда, позволяет использовать в выводе названия векторов данных.
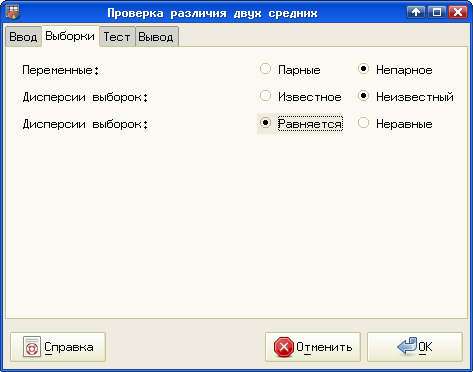
На вкладке "Выборки" (рис. 5.37) указываем, что данные непарные, дисперсии неизвестны, но равны.
На рис. 5.38 показаны результаты вычислений, причем заметно прекрасное согласование результатов с заранее заданными параметрами выборок.
Проделав всё это с любыми модельными данными, в ячейках блока результатов можно увидеть формулы, по которым производятся расчеты.
5.11.2 Неравные выборки, равные дисперсии: T-тест
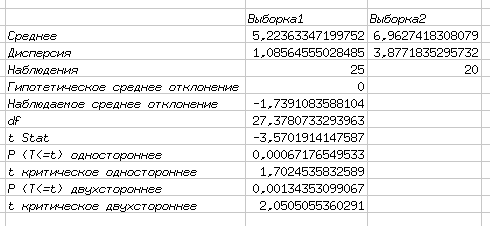
Теперь рассмотрим ситуацию, когда выборки имеют разное количество точек. Пусть параметры Выборки1 остаются прежними (25 точек, нормальное распределение, среднее значение 5 стандартное отклонение 1), а для Выборки2 установим следующие параметры – нормальное распределение со средним 7, стандартным отклонением 1 и количеством точек 20.
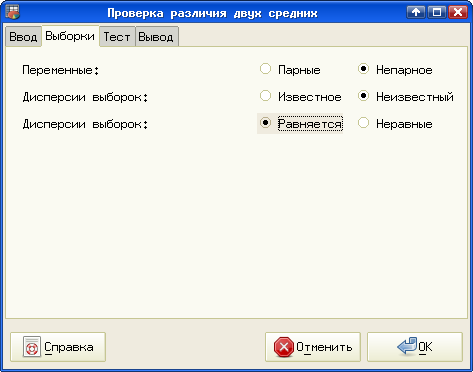
В этом случае на вкладке "Выборки" диалога "Проверка различия двух средних" все оставляем по умолчанию (рис. 5.39), и наблюдаем результаты (рис. 5.40).
Настройки режимов вычислений в этом случае совпадают с предыдущим случаем.
Опять-таки наблюдается соответствие результатов расчетов с заранее определенными параметрами выборок.
5.11.3 Неравные выборки, неравные дисперсии: T-тест
Используя те же параметры распределения для Выборки1, что и в предыдущих случаях, для Выборки2 возьмем 20 точек, среднее значение 7 и стандартное отклонение 2.
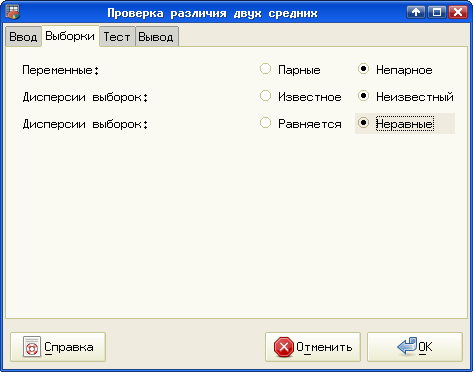
На вкладке "Выборки" установим режимы в соответствии с рис. 5.41 и посмотрим результат (рис. 5.42).
5.11.4 Известные дисперсии: Z-тест
Применим эту процедуру к слегка измененным модельным данным. Пусть Выборка1 остается с прежними параметрами, а для Выборки2 (среднее 7, 20 точек) установим дисперсию 2, для чего стандартное отклонение должно быть установлено как 1,41.
На вкладке "Выборка" устанавливаем режимы и значения дисперсии в соответствии с рис. 5.43 и получаем результат, показанный на рис. 5.44.