Моделирование рисков методом Монте-Карло
В состав Gnumeric входит средство для моделирования по методу Монте-Карло. При использовании метода Монте-Карло используются выборки случайных чисел для решения задач, в которых течение времени не играет существенной роли. Другими словами, на очередную выборку не влияют предыдущие выборки.
При моделировании по методу Монте-Карло используются функции генерации случайных чисел, а результаты представляются вместе со статистическими характеристиками, которые можно затем анализировать.
В данной главе рассмотрен пример из официального руководства по Gnumeric.
9.1 Общее описание задачи
Одна из классических расчётных задач – задача о продавцах газет. Продавцы покупают газеты за 33 цента каждую и продают по 50 центов. Непроданные газеты идут на макулатуру по 5 центов за штуку. Газеты продаются распространителям пачками по 10 штук. Спрос на газеты может быть поделён на "замечательный", "нормальный" и "плохой" с вероятностями 0.35, 0.45 и 0.20 соответственно, причём текущий спрос не зависит от предыдущего дня. Задача продавца – определить оптимальное количество газет в ситуации, когда спрос не вполне известен, то есть добиться устойчивого дохода.
Уравнение для определения дневного дохода для продавца выглядит следующим образом:
Доход=[(Выручка) - (Себестоимость) + (Макулатура)]
Остаётся добавить, что количество закупленных от поставщика газет может изменяться от 40 до 100 включительно, а количество проданных газет также кратно 10.
9.2 Построение модели
Для построения модели в Gnumeric будем использовать два листа – лист "Доход" для вычисления дохода и лист "Таблицы спроса" для таблиц, требуемых для модельных наборов данных, задающих параметры спроса.
На листе "Доход" создадим таблицу расчёта дохода, как показано на рис. 9.1.
Таблицу для вычисления дохода начнём с девятой строки. У нас есть три переменные – выручка от продаж, себестоимость газет и стоимость макулатуры, для которых на каждую единицу товара заданы коэффициенты 0.5, 0.33 и 0.05 соответственно. Запишем эти коэффициенты в ячейки от B13 до D13. В ячейках от B12 до D12 запишем формулы для дохода от продаж, себестоимости и стоимости макулатуры, как показано в таблице 1. В ячейке E12 запишем формулу для вычисления прибыли.
| Адрес ячейки | Значение или формула |
|---|---|
| B12 | =$B$13*min(B16;B20) |
| C12 | =C13*B16 |
| D12 | =D13*max(0;B16-B20) |
| E12 | =B12-C12+D12 |
| B13 | 0,5 |
| C13 | 0,33 |
| D13 | 0,05 |
| B16 | 50 |
Нужно заметить, что на этом этапе в некоторых ячейках появятся сообщения "N/A!" ("нет данных"). Как только модель будет построена полностью, эти сообщения исчезнут.
В ячейке B20 будет задаваться случайное количество проданных газет ("спрос"). Поскольку нельзя продать больше, чем закуплено у поставщика, выручка определяется количеством проданных газет, если закуплено больше, чем продано и ограничивается количеством закупленных газет, если спрос превышает это количество (функция min() при расчёте выручки).
Формула в ячейке D12 означает, что в макулатуру можно сдать только непроданные газеты, поэтому если всё продано (а также если спрос превышает количество закупленных газет), то количество макулатуры будет 0.
Начальное количество закупленных газет установим в 50.
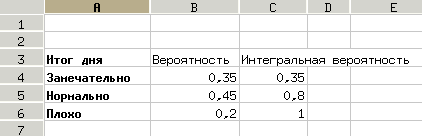
Далее на листе "Таблицы спроса" сформируем модельные параметры спроса в соответствии с рис. 9.2, 9.3 и рис. 9.49.4.
Термин "вероятность" в рассматриваемом примере означает значение функции плотности распределения, а "интегральная вероятность" – значение функции распределения.
На рис. 9.2 показаны плотность распределения и значения функции распределения уровней спроса, на рис 9.3 – функции плотности распределения вероятности продажи заданного количества газет для каждого из вариантов спроса, а на рис. 9.4 – вспомогательные функции распределения вероятностей спроса.
Дополнительными допущениями является то, что 40 газет будут проданы при любых условиях, а вот 100 – только при наиболее благоприятных обстоятельствах.
Теперь снова перейдём на лист "Доход" и продолжим ввод формул, нужных для работы модели. Адреса ячеек и соответствующие формулы показаны в таблице 9.2.
| Адрес ячейки | Значение или формула |
|---|---|
| B17 | =rand() |
| C17 | =if(B17<'Таблицы спроса'!C4;"Замечательно";if(B17< 'Таблицы спроса'!C5;"Нормально";"Плохо")) |
| B18 | =rand() |
| B20 | =lookup(C17;$B$23:$D$23;$B$24:$D$24) |
| B21 | =E12 |
| B23 | Замечательно |
| C23 | Нормально |
| D23 | Плохо |
| B24 | =lookup($B$18;'Таблицы спроса'!$E$23:$E$29;'Таблицы спроса'!$A$23:$A$29) |
| C24 | =lookup($B$18;'Таблицы спроса'!$F$23:$F$29;'Таблицы спроса'!$A$23:$A$29) |
| D24 | =lookup($B$18;'Таблицы спроса'!$G$23:$G$29;'Таблицы спроса'!$A$23:$A$29) |
Случайное число в ячейке B17 определяет уровень (состояние) спроса, который выводится в ячейку C17. Случайное число в ячейке B18 определяет количества проданных газет для каждого уровня спроса (ячейки B24, C24 и D24). В соответствии с ранее заданным в C17 уровнем спроса в ячейке B20 получаем текущий спрос на газеты, из которого уже рассчитывается доход.
Итоговый вариант листа "Доход" должен выглядеть примерно так, как показано на рис. 9.5.
Нажимая на клавишу F9 ("Правка/Пересчитать" в главном меню) можем наблюдать за изменением чисел и, соответственно, за изменением дохода.