Инструменты Gnumeric для статистиков
5.2 Прогнозирование
Статистическое прогнозирование (в англоязычных статистических программах – forecasting) является на самом деле сглаживанием, которое применяется для выделения тенденции при сильном разбросе точек исходных данных. В Gnumeric эта процедура может проводиться двумя способами – методом экспоненциального сглаживания и методом скользящего среднего (соответственно, команды главного меню "Статистика/Зависимые наблюдения/Прогнозирование/Экспоненциальное сглаживание..." и "Статистика/Зависимые наблюдения/Прогнозирование/Скользящее среднее..."). При выборе сглаживания методом скользящего среднего можно указать количество точек, по которым будет проводиться усреднение.
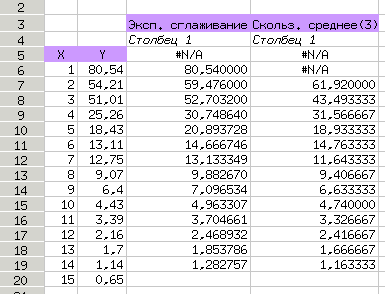
Рассмотрим пример с некоторыми экспериментальными данными (рис. 5.10). Вектор  представляет собой некоторую независимую переменную, вектор
представляет собой некоторую независимую переменную, вектор  – измеренные значения. Правее приведены результаты экспоненциального сглаживания и сглаживания методом скользящего среднего по трем точкам. Поскольку при сглаживании для данного значения
– измеренные значения. Правее приведены результаты экспоненциального сглаживания и сглаживания методом скользящего среднего по трем точкам. Поскольку при сглаживании для данного значения  оказываются задействованы предыдущие и последующие значения, то количество "сглаженных" точек меньше, чем количество исходных. Это видно как по отсутствию последнего значения в обоих случаях сглаживания, так и из сообщения "#N/A (нет данных)" в начале последовательности. Для скользящего среднего по трем точкам результат вообще начинается только с третьей точки последовательности.
оказываются задействованы предыдущие и последующие значения, то количество "сглаженных" точек меньше, чем количество исходных. Это видно как по отсутствию последнего значения в обоих случаях сглаживания, так и из сообщения "#N/A (нет данных)" в начале последовательности. Для скользящего среднего по трем точкам результат вообще начинается только с третьей точки последовательности.
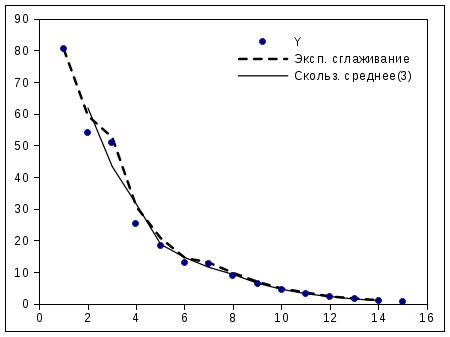
График исходных данных и результатов сглаживания показан на рис. 5.11. Нужно заметить, что сами операции сглаживания ("прогнозирования") дают только числовые значения.
Из графика видно, что скользящее среднее (сплошная линия) в данном примере дает лучший результат, но чем больше точек участвуют в усреднении (и чем более гладкой получается кривая), тем больше точек в начале и в конце теряются.