Инструменты Gnumeric для статистиков
5.5 Регрессия
Регрессия как элемент статистического анализа в Gnumeric проводится по линейной модели, а отклонения рассматриваются как нормально распределённые случайные ошибки. В результате проведения такого регрессионного анализа ("Статистика/Зависимые наблюдения/Регрессия...") вычисляется множество параметров.
Рассмотрим результаты регрессии для примера исходных данных, использованных ранее для сглаживания (см. рис. 5.10).
При создании иллюстрации (рис. 5.15) данные из длинных строчек (параметры "F" и "P") были перенесены вниз, т.е. в реальной таблице ячейки "F" и "Значимость F" находятся в той же строке, что и параметр "степень свободы", а значения параметров "P", "Ниже 95%" и "Выше 95%" - в тех же строках, что и значения коэффициентов регрессии.
По результатам выполнения регрессии можно получить следующее уравнение  . Параметр "Столбец1" дает коэффициент наклона прямой, а параметр "Пересечение" – точку пересечения прямой с осью
. Параметр "Столбец1" дает коэффициент наклона прямой, а параметр "Пересечение" – точку пересечения прямой с осью  .
.
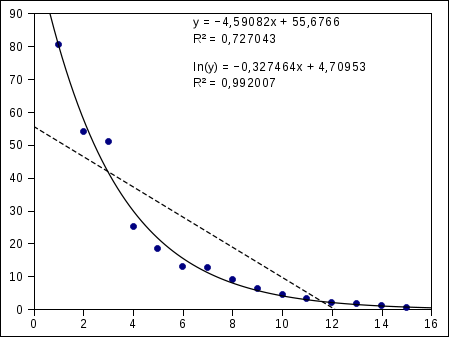
Интересно сравнить результаты регрессионного анализа, проведенного таким образом, с уравнениями регрессии, которые можно получить на диаграмме XY (рис. 5.16).
На рис. 5.16 точками показаны исходные данные, пунктирной линией – линейная регрессия (верхнее уравнение), параметры которой в точности совпадают с вычисленными с помощью "статистического" регрессионного анализа. Сплошная линия и нижнее уравнение соответствуют экспоненциальной модели регрессии, которая дает гораздо лучший коэффициент определенности (критерий Пирсона).
Более подробно построение кривых регрессии будет рассматриваться в главе "Регрессионный анализ в Gnumeric".
5.6 Анализ Фурье
Модуль преобразования Фурье ("Статистика/Зависимые наблюдения/Анализ Фурье...") позволяет вычислять дискретное преобразование Фурье (ДПФ) для заданного ряда данных (режим "Инверсия" на вкладке "Параметры" диалога "Анализ Фурье" позволяет, по-видимому, вычислять обратное преобразование Фурье).
Рассмотрим два примера. Первый пример – преобразование Фурье для гауссовой кривой, задаваемой формулой (5.1).
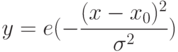 |
( 5.1) |
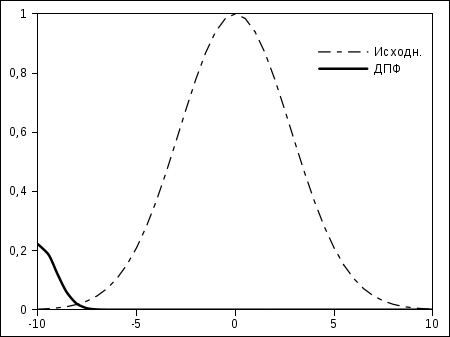
Известно, что для такой функции Фурье-образ будет иметь вид такой же функции (с точностью до нормировки). Путь для простоты x0 имеет значение 0, а дисперсия пусть будет равна 4. Графики исходной функции (пунктир) и ее Фурье-образа (сплошная линия) показаны на рис. 5.17.
В Gnumeric вычисляются действительная и мнимая части Фурье-образа, так что для получения окончательного результата можно воспользоваться математической функцией hypot(), вычисляющей квадратный корень из суммы квадратов аргументов.
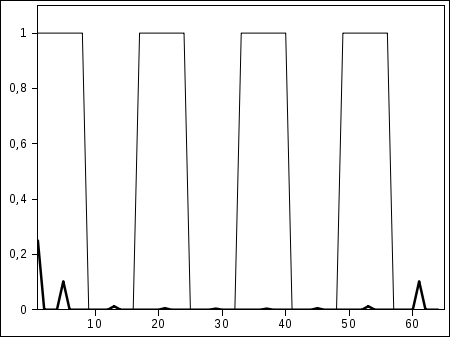
Теперь попробуем получить Фурье-образ для периодической "прямоугольной" функции (прямоугольных импульсов), причем состояние "0" и состояние "1" длятся по половине периода (рис. 5.18).
По горизонтальной оси отложены некие условные единицы. Период исходной функции составляет 16 единиц (всего взято 64 точки). Фурье-образ показан более жирной линией. Видно, что Фурье-образ симметричен относительно середины горизонтальной оси. Чем больше точек по горизонтали взято и чем больше период исходной функции, тем больше компонентов ряда Фурье можно различить.
Специально для читателей с инженерным и техническим образованием нужно заметить, что на рис. 5.18 показан квадрат модуля Фурье-образа, что соответствует, например, распределению энергии при дифракции электромагнитных волн на периодической решетке. В полном соответствии с теорией дифракции для заданных параметров решетки "энергия" в первом порядке (первый слева пик) составляет около 10% абсолютной величины.