Основы работы в Gnumeric

2.6.3 Функции комплексного переменного.

Функций работы с комплексными числами в Gnumeric насчитывается более сорока, поэтому здесь рассмотрим только основные (и наиболее интересные с точки зрения автора).

Таблица 2.4. Функции работы с комплексными числами

Название, аргументы	Назначение
complex(x1;x2;символ)	Формирует комплексное число из двух вещественных. Третий необязательный аргумент (символ) позволяет изменить обозначение мнимой единицы. Если он не указан, будет сформировано комплексное число вида .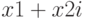
imabs(complex)	Вычисляет модуль комплексного числа. Например, если в ячейке E3 записано комплексное число 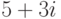(как результат функции complex()), то imabs(E3) выдаст 5,83095.
imargument(complex)	Вычисляет аргумент комплексного числа (показатель степени при экспоненциальном представлении). Для примера 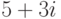выдаст значение 0,54042.
imreal(complex)	Выдает вещественную часть комплексного числа.
imaginary(complex)	Выдает мнимую часть комплексного числа.
imconjugate(complex)	Вычисляет комплексно сопряженное число.
imdiv(complex1;complex2)	Вычисляет целую часть результата деления двух комплексных чисел.
iminv(complex)	Выполняет преобразование .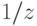
impower(complex;power)	Возводит комплексное число в степень, которая тоже может быть комплексным числом.
improduct(complex1;complex2;...)	Вычисляет произведение комплексных чисел (обычная операция умножения не работает!).

Далее рассмотрим использование логических и математических функций, а также функций комплексного переменного на классическом примере вычисления корней квадратного уравнения с произвольными коэффициентами.

Рис. 2.55. Решение квадратного уравнения

Итак, заданы три коэффициента и квадратного уравнения вида

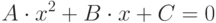( 2.1)

Требуется вычислить корни и , которые в общем случае могут быть комплексными. Перед вычислением корней вычислим дискриминант :

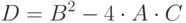( 2.2)

И затем воспользуемся формулой для вычисления корней:

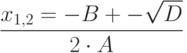( 2.3)

Однако при отрицательном дискриминанте корни будут комплексными. Такое комплексное число будет иметь вещественную часть и мнимую часть (с точностью до знака)

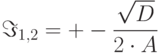( 2.4)

В то же время для неотрицательных значений дискриминанта будут работать обычные правила вычисления корней (в соответствии с формулой (2.3)). Таким образом, в формуле для вычисления корня должна присутствовать проверка дискриминанта на отрицательность, и при отрицательном дискриминанте должно быть сформировано комплексное число. При неотрицательном дискриминанте используются обычные функции и арифметические действия.

После столь долгих рассуждений пора показать таблицу и формулы для вычислений (рис. 2.55).

Формулы для вычислений приведены ниже: