Инспектор
Вы можете этот курс.
Опубликован: 24.04.2015 | Уровень: для всех | Доступ: платный
Лекция 2:
Основы работы в Gnumeric
Текстовые (строковые) функции
Одна из типовых задач в офисной работе – изменения формы представления списков людей или организаций. Избежать трудоёмкой работы по переписыванию текста из одного вида в другой помогают функции работы с текстом (строковые функции).
Почему-то подобные задачи кажутся очень сложными, поэтому покажем пример решения и рассмотрим минимальный набор функций, необходимых для получения результата.
Пусть имеется список лиц с полными фамилиями, именами и отчествами (например, список группы слушателей каких-нибудь курсов). Для составления журнала полные имена и отчества не требуются, а требуются только инициалы. Задача заключается в преобразовании имён и отчеств в буквы инициалов.
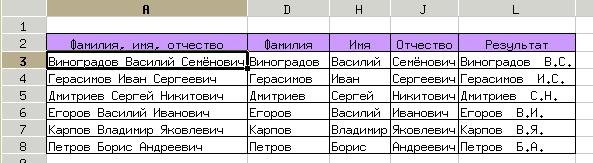
На рис. 2.66 показан пример решения такой задачи. Следует обратить внимание, что имеются скрытые столбцы, в которых содержатся результаты промежуточных вычислений.
Алгоритм решения задачи может быть таким:
- Определяем длину строки "Фамилия, имя, отчество"
- Определяем длину фамилии (количество букв до первого пробела)
- Делим строку "Фамилия, имя, отчество" на фамилию и всё что осталось (получаются строки "Фамилия" и "Имя, отчество")
- Определяем длину строки "Имя, отчество"
- Определяем длину имени (количество букв до первого пробела в строке "Имя, отчество")
- Делим строку "Имя, отчество" на имя и всё что осталось (получаются строки "Имя" и "Отчество")
- Выделяем первую букву имени
- Выделяем первую букву отчества
- Создаём итоговую строку из строки "Фамилия" и первых букв имени и отчества
Строковые функции, которые понадобятся для решения данной задачи, описаны в таблице ниже.
| Название, аргументы | Назначение |
|---|---|
| len(str) | Вычисляет длину (количество символов) для строки str. |
| find(str1;str2;start) | Определяет позицию (номер символа), с которой начинается подстрока str1 в строке str2, начиная с позиции start. Если аргумент start не указан, поиск идёт с начала строки. |
| left(str;n) | Выделяет n символов с начала строки str. Если аргумент n не указан, функция возвращает первый символ строки. |
| right(str;n) | Выделяет n символов с конца строки str. Если аргумент n не указан, функция возвращает последний символ строки. |
| concatenate(str1;str2;...;strN) | Формирует одну строку из "фрагментов" – строк str1, str2, …, strN. |
В следующей таблице приведены формулы, использованные при решении задачи.
| Адрес ячейки, назначение | Формула |
|---|---|
| =len(A3) | B3: Длина исходной строки |
| =find(" ";A3) | C3: Позиция первого пробела (количество букв в фамилии) |
| =left(A3;C3) | D3: Строка "Фамилия" |
| =right(A3;B3-C3) | E3: Строка "Имя, отчество" |
| =len(E3) | F3: Длина строки"Имя, отчество" |
| =find(" ";E3) | G3: Позиция первого пробела в строке "Имя, отчество" (количество букв в имени) |
| =left(E3;G3) | H3: Строка "Имя" |
| =left(H3) | I3: Первая буква имени |
| =right(E3;F3-G3) | J3: Строка "Отчество" |
| =left(J3) | K3: Первая буква отчества |
| =concatenate(D3;" ";I3;".";K3;".") | L3: Результат |
Символьные (строковые) значения в формулах (в аргументах функций) следует указывать в кавычках.
В качестве других полезных строковых функций (по мнению автора) нужно отметить функции преобразования регистров lower() (переводит все символы строки в нижний регистр, т. е. в строчные буквы) и upper() (переводит все символы строки в верхний регистр, т. е. в прописные буквы), функцию mid(), которая позволяет вывести заданное количество символов строки, начиная с заданного символа, а также функцию value(), превращающую строку из символов-цифр в число.
2.6.8 Обработка матриц
Gnumeric обеспечивает базовые возможности по работе с матрицами. Список функций приведён в таблице ниже. Все эти функции в качестве аргументов используют диапазоны ячеек, в которые записаны элементы матриц.
| Название, аргументы | Назначение |
|---|---|
| transpose(matrix) | Выполняет транспонирование матрицы matrix (строки становятся столбцами и наоборот). Функция находиться в категории "Поиск". |
| mdeterm(matrix) | Вычисляет определитель квадратной матрицы. |
| minverse(matrix) | Вычисляет матрицу, обратную по отношению к исходной, при условии, что определитель не равен нулю. |
| mmult(matrix1;matrix2) | Вычисляет матричное произведение. Результирующая матрица имеет количество строк как в matrix1 и столбцов как в matrix2. |
Чтобы в результате операций с матрицами получить тоже матрицу (если это нужно), в "Помощнике по формулам" нужно установить режим "Ввести как функцию массива" (рис. 2.67).
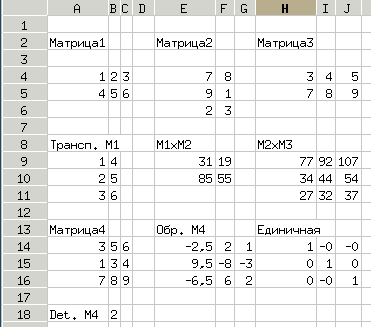
Пример вычислений с матрицами показан на рис. 2.68.
В Gnumeric отсутствует функция для создания единичной матрицы, но такая матрица легко может быть получена умножением произвольной матрицы на обратную ей, что и проиллюстрировано на рис. 2.68 (здесь -0 указывает на то, что в результате погрешностей вычислений в связи с ограниченной точностью представления получилось вещественное отрицательное число с очень маленьким модулем).
