НОУ ИНТУИТ | Практикум по методам построения алгоритмов. Лекция 15: Контекстно-свободные грамматики

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 08.04.2009 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 24 студентам

| Поделиться |

Поддержать программу

15.3. Алгоритм разбора для LL(1)-грамматик

В этом разделе мы рассмотрим еще один метод проверки выводимости в КС-грамматике, называемый по традиции LL(1)-разбором. Вот его идея в одной фразе: можно считать, что в процессе вывода мы всегда заменяем самый левый нетерминал и нужно лишь выбрать одно из правил; если нам повезет с грамматикой, то выбрать правило можно, глядя на первый символ выводимого из этого нетерминала слова. Говоря более формально, дадим такое

Определение. Левым выводом (слова в грамматике) называется вывод, в котором на каждом шаге замене подвергается самый левый из нетерминалов.

15.3.1. Для каждого выводимого слова (из терминалов) существует его левый вывод.

Решение. Различные нетерминалы заменяются независимо; если в процессе вывода появилось слово 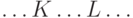$\ldots K\ldots L\ldots$ , где , - нетерминалы, то замены и можно производить в любом порядке. Поэтому можно перестроить вывод так, чтобы стоящий левее нетерминал заменялся раньше. (Формально говоря, надо доказывать индукцией по длине вывода такой факт: если из некоторого нетерминала выводится некоторое слово , то существует левый вывод из .)

15.3.2. В грамматике с 4 правилами

$\begin{multiple} && (1)\quad \hbox{\texttt{E}} \to \\ && (2)\quad \hbox{\texttt{E}} \to \hbox{\texttt{TE}}\\ && (3)\quad \hbox{\texttt{T}} \to \hbox{\texttt{(E)}}\\ && (4)\quad \hbox{\texttt{T}} \to \hbox{\texttt{[E]}} \end{multiple}$

найти левый вывод слова $A ={\texttt{[()([\,])]}}$ и доказать, что он единствен.

Решение. На первом шаге можно применить только правило (2):

${\texttt{E}} \to {\texttt{TE}}$

Что будет дальше с T? Так как слово

начинается на [, то может примениться только правило (4):

${\texttt{E}} \to {\texttt{TE}}\to {\texttt{[E]E}}$

Первое E должно замениться на TE (иначе вторым символом была бы скобка ] ):

${\texttt{E}} \to {\texttt{TE}}\to{\texttt{[E]E}} \to{\texttt{[TE]E}}$

и T должно заменяться по (3):

${\texttt{E}}\to{\texttt{TE}}\to{\texttt{[E]E}} \to{\texttt{[TE]E}}\to{\texttt{[(E)E]E}}$

Далее первое E должно замениться на пустое слово (иначе третьей буквой слова будет ( или [ - только на эти символы может начинаться слово, выводимое из T ):

${\texttt{E}}\to{\texttt{TE}}\to{\texttt{[E]E}}\to{\texttt{[TE]E}}\to{\texttt{[(E)E]E}}\to{\texttt{[()E]E}}$

и далее

$\begin{multiline*} \ldots\to \hbox{\texttt{[()TE]E}} \to\hbox{\texttt{[()(E)E]E}} \to\hbox{\texttt{[()(TE)E]E}} \to\hbox{\texttt{[()([E]E)E]E}}\to{}\\ % \to\hbox{\texttt{[()([\,]E)E]E}} \to\hbox{\texttt{[()([\,])E]E}} \to\hbox{\texttt{[()([\,])]E}} \to\hbox{\texttt{[()([\,])]}} \end{multiline*}$

Что требуется от грамматики, чтобы такой метод поиска левого вывода был применим? Пусть, например, на очередном шаге самым левым нетерминалом оказался нетерминал , т.е. мы имеем слово вида AKU , где - слово из терминалов, а - слово из терминалов и нетерминалов. Пусть в грамматике есть правила

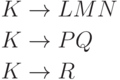
$\begin{align*} K&\to L M N\\ K&\to P Q\\ K&\to R \end{align*}$

Нам надо выбрать одно из них. Мы будем пытаться сделать этот выбор, глядя на первый символ той части входного слова, которая выводится из

.

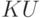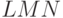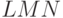Рассмотрим множество Нач(LMN) тех терминалов, с которых начинаются непустые слова, выводимые из LMN . (Это множество равно Нач(L), объединенному с Нач(M), если из выводится пустое слово, а также с Нач(N), если из и из выводится пустое слово.) Чтобы описанный метод был применим, надо, чтобы Нач(LMN), Нач(PQ) и Нач(R) не пересекались. Но этого мало. Ведь может быть так, например, что из LMN будет выведено пустое слово, а из слова будет выведено слово, начинающееся на букву из Нач(PQ). Следующие определения учитывают эту проблему.

Напомним, что определение выводимости в КС-грамматике было дано только для слова из терминалов. Оно очевидным образом обобщается на случай слов из терминалов и нетерминалов. Можно также говорить о выводимости одного слова (содержащего терминалы и нетерминалы) из другого. (Если говорится о выводимости слова без указания того, откуда оно выводится, то всегда подразумевается выводимость в грамматике, т.е. выводимость из начального нетерминала.)

Для каждого слова из терминалов и нетерминалов через Нач(X) обозначаем множество всех терминалов, с которых начинаются непустые слова из терминалов, выводимые из . (В случае, если из любого нетерминала выводится хоть одно слово из терминалов, не играет роли, рассматриваем ли мы при определении Нач(X) слова только из терминалов или любые слова. Мы будем предполагать далее, что это условие выполнено.)

Для каждого нетерминала через Послед(K) обозначим множество терминалов, которые встречаются в выводимых (в грамматике) словах сразу же за . (Не смешивать с Посл(K) предыдущего раздела!) Кроме того, в Послед(K) включается символ EOI, если существует выводимое слово, оканчивающееся на .

Для каждого правила

$K \to V$

(где

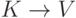
- нетерминал,

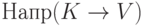- слово, содержащее терминалы и нетерминалы) определим множество направляющих терминалов, обозначаемое $Напр(K\to V)$ . По определению оно равно Нач(V)

, к которому добавлено Послед(K)

, если из

выводится пустое слово.

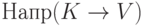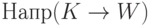Определение. Грамматика называется LL(1)-грамматикой, если для любых правил $K\to V$ и $K\to W$ с одинаковыми левыми частями множества $Напр(K\to V)$ и $Напр(K\to W)$ не пересекаются.