Практикум по методам построения алгоритмов

:

Практикум по методам построения алгоритмов
[+]
Опубликован: 08.04.2009 | Уровень: для всех | Доступ: платный
Лекция 15:

Контекстно-свободные грамматики
A
|
версия для печати
< Лекция 14 || Лекция 15: 1234567 || Лекция 16 >

15.1.4. Привести пример другой грамматики, задающей тот же язык.

Ответ. Вот один из вариантов:

\begin{align*} \langle{выр}\rangle &\to\langle{выр}\rangle\ \hbox{\texttt{+}}\ \langle{выр}\rangle\\ \langle{выр}\rangle &\to\langle{выр}\rangle\ \hbox{\texttt{*}}\ \langle{выр}\rangle\\ \langle{выр}\rangle &\to \hbox{\texttt{x}}\\ \langle{выр}\rangle &\to \hbox{\texttt{(}}\ \langle{выр}\rangle\ \hbox{\texttt{)}} \end{align*}

Эта грамматика хоть и проще, но в некоторых отношениях хуже, о чем мы еще будем говорить.

15.1.5. Дана произвольная КС-грамматика. Построить алгоритм проверки принадлежности задаваемому ей языку, работающий полиномиальное время (т.е. число действий не превосходит полинома от длины проверяемого слова; полином может зависеть от грамматики).

Решение. Заметим, что требование полиномиальности исключает возможность решения, основанном на переборе всех возможных выводов. Тем не менее полиномиальный алгоритм существует. Поскольку практического значения он не имеет (используемые на практике КС-грамматики обладают дополнительными свойствами, позволяющими строить более эффективные алгоритмы), мы изложим лишь общую схему решения.

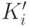(1) Пусть в грамматике есть нетерминалы K_1,\ldots,K_n. Построим новую грамматику с нетерминалами K_1',\ldots,K_n' так, чтобы выполнялось такое свойство: из K_i' выводятся (в новой грамматике) те же слова, что из 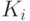K_i в старой, за исключением пустого слова, которое не выводится.

Чтобы выполнить такое преобразование грамматики, надо выяснить, из каких нетерминалов исходной грамматики выводится пустое слово, а затем каждое правило заменить на совокупность правил, получающихся, если в правой части опустить какие-либо из нетерминалов, из которых выводится пустое слово, а у остальных поставить штрихи. Например, если в исходной грамматике было правило

\begin{center}\ttfamily K \to L M N, \end{center}
причем из L и N выводится пустое слово, а из M нет, то это правило надо заменить на правила
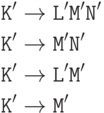
\begin{align*} \hbox{\texttt{K}}' &\to \hbox{\texttt{L}}'\hbox{\texttt{M}}'\hbox{\texttt{N}}'\\ \hbox{\texttt{K}}' &\to \hbox{\texttt{M}}'\hbox{\texttt{N}}'\\ \hbox{\texttt{K}}' &\to \hbox{\texttt{L}}'\hbox{\texttt{M}}'\\ \hbox{\texttt{K}}' &\to \hbox{\texttt{M}}' \end{align*}

(2) Итак, мы свели дело к грамматике, где ни из одного нетерминала не выводится пустое слово. Теперь устраним "циклы" вида

\begin{align*} \texttt{K} &\to \texttt{L} \\ \texttt{L} &\to \texttt{M} \\ \texttt{M} &\to \texttt{N} \\ \texttt{N} &\to \texttt{K} \end{align*}
(в правой части каждого правила один символ, и эти символы образуют цикл произвольной длины): это легко сделать, отождествив все входящие в цикл нетерминалы.

(3) Теперь проверка принадлежности какого-либо слова языку, порожденному грамматикой, может выполняться так: для каждого подслова проверяемого слова и для каждого нетерминала выясняем, порождается ли это подслово этим нетерминалом. При этом подслова проверяются в порядке возрастания длин, а нетерминалы - в таком порядке, чтобы при наличии правила K \to L нетерминал L проверялся раньше нетерминала K. (Это возможно в силу отсутствия циклов.) Поясним этот процесс на примере.

Пусть в грамматике есть правила

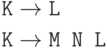
\begin{align*} \texttt{K} &\to \texttt{L}\\ \texttt{K} &\to \texttt{M N L} \end{align*}
и других правил, содержащих K в левой части, нет. Мы хотим узнать, выводится ли данное слово A из нетерминала K. Это будет так в одном из случаев:

  • если A выводится из L ;
  • если A можно разбить на непустые слова B, C, D, для которых B выводится из M, C выводится из N, а D выводится из L.

Вся эта информация уже есть (слова B, C, D короче A, а L рассмотрен до K ).

Легко видеть, что число действий этого алгоритма полиномиально. Степень полинома зависит от числа нетерминалов в правых частях правил и может быть понижена, если грамматику преобразовать к форме, в которой правая часть каждого правила не более 2 нетерминалов (это легко сделать, вводя новые нетерминалы: например, правило K \to LMK можно заменить на K \to LN и N \to MK, где N - новый нетерминал).

15.1.6. Рассмотрим грамматику с единственным нетерминалом K, нетерминалами 1, 2, 3 и правилами

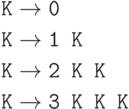
\begin{align*} \texttt{K} &\to \texttt{0}\\ \texttt{K} &\to \texttt{1 K}\\ \texttt{K} &\to \texttt{2 K K}\\ \texttt{K} &\to \texttt{3 K K K} \end{align*}
Как проверить выводимость слова в этой грамматике, читая слово слева направо? (Число действий при прочтении одной буквы должно быть ограничено.)

Решение. Хранится целая переменная n, инвариант: слово выводимо \Leftrightarrow непрочитанная часть представляет собой конкатенацию (соединение) n выводимых слов.

15.1.7. Тот же вопрос для грамматики

\begin{align*} \texttt{K} &\to \texttt{0}\\ \texttt{K} &\to \texttt{K 1}\\ \texttt{K} &\to \texttt{K K 2}\\ \texttt{K} &\to \texttt{K K K 3} \end{align*}

Дальше >>
< Лекция 14 || Лекция 15: 1234567 || Лекция 16 >

Вопросы и ответы

вопросов: 0

Студенты

всего: 18
Татьяна Новикова
Татьяна Новикова
Россия, Пошатово
предложить дружбу
Artem Bardakov
Artem Bardakov
Россия
предложить дружбу