| Россия, Пошатово |
Рекурсия
7.1. Примеры рекурсивных программ
При анализе рекурсивной программы возникает, как обычно, два вопроса:
- почему программа заканчивает работу?
- почему она работает правильно, если заканчивает работу?
Для (2) достаточно проверить, что (содержащая рекурсивный вызов) программа работает правильно, предположив, что вызываемая ею одноименная программа работает правильно. В самом деле, в этом случае в цепочке рекурсивно вызываемых программ все программы работают правильно (убеждаемся в этом, идя от конца цепочки к началу).
Чтобы доказать (1), обычно проверяют, что с каждым рекурсивным вызовом значение какого-то параметра уменьшается, и это не может продолжаться бесконечно.
7.1.1.
Написать рекурсивную процедуру вычисления факториала целого
положительного числа  (т. е. произведения
(т. е. произведения 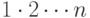 , обозначаемого
, обозначаемого  !).
!).
Решение. Используем равенства 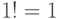 ,
, 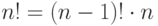 .
.
procedure factorial (n: integer; var fact: integer);
| {положить fact равным факториалу числа n}
begin
| if n=1 then begin
| | fact:=1;
| end else begin {n>1}
| | factorial (n-1, fact);
| | {fact = (n-1)!}
| | fact:= fact*n;
| end;
end;С использованием процедур-функций можно написать так:
function factorial (n: integer): integer;
begin
| if n=1 then begin
| | factorial:=1;
| end else begin {n>1}
| | factorial:= factorial (n-1)*n;
| end;
end;Обратите внимание на некоторую двойственность использования
имени  внутри описания функции: оно обозначает
как переменную, так и вызываемую рекурсивно функцию.
К счастью, в нашем случае они различаются по скобкам после
имени, но если бы функция была без параметров, то дело было
бы плохо. (Стандартная, но трудно находимая ошибка
возникает, если автор программы на паскале полагает, что он
использует значение переменной, а компилятор в этом месте
видит рекурсивный вызов.)
внутри описания функции: оно обозначает
как переменную, так и вызываемую рекурсивно функцию.
К счастью, в нашем случае они различаются по скобкам после
имени, но если бы функция была без параметров, то дело было
бы плохо. (Стандартная, но трудно находимая ошибка
возникает, если автор программы на паскале полагает, что он
использует значение переменной, а компилятор в этом месте
видит рекурсивный вызов.)
7.1.2.
Обычно факториал определяют и для нуля, считая, что 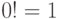 . Изменить программы соответственно.
. Изменить программы соответственно.
7.1.3. Написать рекурсивную программу возведения в целую неотрицательную степень.
7.1.4.
То же, если требуется, чтобы глубина рекурсии не
превосходила  , где
, где  - показатель степени.
- показатель степени.
Решение.
function power (a,n: integer): integer; begin | if n = 0 then begin | | power:= 1; | end else if n mod 2 = 0 then begin | | power:= power(a*a, n div 2); | end else begin | | power:= power(a, n-1)*a; | end; end;
7.1.5. Что будет, если изменить программу, приведенную в решении предыдущей задачи, заменив строку
power:= power(a*a, n div 2)
на
power:= power(a, n div 2)* power(a, n div 2)?
Решение. Программа останется правильной. Однако она станет работать медленнее. Дело в том, что теперь вызов может породить два вызова (хотя и одинаковых) вместо одного - и число вызовов быстро растет с глубиной рекурсии. Программа по-прежнему имеет логарифмическую глубину рекурсии, но число шагов работы становится линейным вместо логарифмического.
Этот недостаток можно устранить, написав
t:= power(a, n div 2); power:= t*t;
или воспользовавшись функцией возведения в квадрат  .
.
7.1.6.
Используя команды  лишь при
лишь при 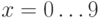 ,
написать рекурсивную программу печати десятичной записи
целого положительного числа
,
написать рекурсивную программу печати десятичной записи
целого положительного числа  .
.
Решение. Здесь использование рекурсии облегчает жизнь (проблема была в том, что цифры легче получать с конца, а печатать надо с начала).
procedure print (n:integer); {n>0}
begin
| if n<10 then begin
| | write (n);
| end else begin
| | print (n div 10);
| | write (n mod 10);
| end;
end;7.1.7.
Игра "Ханойские башни" состоит в следующем. Есть
три стержня. На первый из них надета пирамидка из  колец
(большие кольца снизу, меньшие сверху). Требуется
переместить кольца на другой стержень. Разрешается
перекладывать кольца со стержня на стержень, но класть
большее кольцо поверх меньшего нельзя. Составить программу,
указывающую требуемые действия.
колец
(большие кольца снизу, меньшие сверху). Требуется
переместить кольца на другой стержень. Разрешается
перекладывать кольца со стержня на стержень, но класть
большее кольцо поверх меньшего нельзя. Составить программу,
указывающую требуемые действия.
Решение. Напишем рекурсивную процедуру перемещения  верхних колец с
верхних колец с 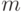 -го стержня на
-го стержня на 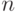 -ый
(остальные кольца предполагаются большими по размеру
и лежат на стержнях без движения).
-ый
(остальные кольца предполагаются большими по размеру
и лежат на стержнях без движения).
procedure move(i,m,n: integer);
| var s: integer;
begin
| if i = 1 then begin
| | writeln ('сделать ход ', m, '->', n);
| end else begin
| | s:=6-m-n; {s - третий стержень: сумма номеров равна 6}
| | move (i-1, m, s);
| | writeln ('сделать ход ', m, '->', n);
| | move (i-1, s, n);
| end;
end;(Сначала переносится пирамидка из  колец на третью
палочку. После этого
колец на третью
палочку. После этого  кольцо
освобождается, и его можно перенести куда следует. Остается
положить на него пирамидку.)
кольцо
освобождается, и его можно перенести куда следует. Остается
положить на него пирамидку.)
7.1.8.
Написать рекурсивную программу суммирования массива ![\text{a: array [1..n] of integer}](/sites/default/files/tex_cache/42384a44c8fa5fa7ecb8c5f3a8ce5edf.png) .
.
Указание. Рекурсивно определяемая функция должна иметь дополнительный параметр - число складываемых элементов.
