Типы данных

6.4. Разные задачи

6.4.1. Реализовать структуру данных, которая имеет все те же операции, что массив длины n, а именно

• начать работу;
• положить в i -ю ячейку число x ;
• узнать, что лежит в i -ой ячейке;

а также операцию

• указать номер минимального элемента

(точнее, одного из минимальных элементов). Количество действий для всех операций должно быть не более , не считая операции "начать работу" (которая требует не более Cn действий).

Решение. Используется прием, изложенный в разделе о сортировке деревом. Именно, надстроим над элементами массива как над листьями двоичное дерево, в каждой вершине которого храним минимум элементов соответствующего поддерева. Корректировка этой информации, а также прослеживание пути из корня к минимальному элементу требуют логарифмического числа действий.

6.4.2. Приоритетная очередь - это очередь, в которой важно не то, кто встал последним (порядок помещения в нее не играет роли), а кто главнее. Более точно, при помещении в очередь указывается приоритет помещаемого объекта (будем считать приоритеты целыми числами), а при взятии из очереди выбирается элемент с наибольшим приоритетом (или один из таких элементов). Реализовать приоритетную очередь так, чтобы помещение и взятие элемента требовали логарифмического числа действий (от размера очереди).

Решение. Следуя алгоритму сортировки деревом (в его окончательном варианте), будем размещать элементы очереди в массиве x[1..k], поддерживая такое свойство: x[i] старше (имеет больший приоритет) своих сыновей x[2i] и x[2i+1], если таковые существуют - и, следовательно, всякий элемент старше своих потомков. 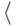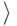(Сведения о приоритетах также хранятся в массиве, так что мы имеем дело с массивом пар элемент, приоритет .) Удаление элемента с сохранением этого свойства описано в алгоритме сортировки. Надо еще уметь восстанавливать свойство после добавления элемента в конец. Это делается так:

t:= номер добавленного элемента
{инвариант: в дереве любой предок приоритетнее потомка,
    если этот потомок - не t}
while t - не корень и t старше своего отца do begin
| поменять t с его отцом
end;

Если очередь образуют граждане, стоящие в вершинах дерева, т.е. за каждым стоит двое, а перед каждым (кроме первого) - один, то смысл этого алгоритма ясен: встав в конец, приоритетный гражданин начинает пробираться к началу, вытесняя впереди стоящих - пока не встретит более приоритетного.

Замечание. Приоритетную очередь естественно использовать при моделировании протекающих во времени процессов. При этом элементы очереди - это ожидаемые события, а их приоритет определяется временем, когда они произойдут.