Типы данных

Применение очередей

6.2.5. Напечатать в порядке возрастания первые n натуральных чисел, в разложение которых на простые множители входят только числа 2, 3, 5.

Решение. Введем три очереди x2, x3, x5, в которых будем хранить элементы, которые в 2 ( 3, 5 ) раз больше напечатанных, но еще не напечатаны. Определим процедуру

procedure напечатать_и_добавить (t: integer);
begin
| writeln (t);
| Добавить (2*t, x2);
| Добавить (3*t, x3);
| Добавить (5*t, x5);
end;

Вот схема программы:

...сделать x2, x3, x5 пустыми
напечатать_и_добавить (1);
k := 1; { k - число напечатанных }
{инвариант: напечатано в порядке возрастания k минимальных
членов нужного множества; в очередях элементы, вдвое,
втрое и впятеро большие напечатанных, но не напечатанные,
расположенные в возрастающем порядке}
while k <> n do begin
| x := min (очередной(x2), очередной(x3), очередной(x5));
| напечатать_и_добавить (x);
| k := k+1;
| ...взять x из тех очередей, где он был очередным;
end;

Пусть инвариант выполняется. Рассмотрим наименьший из ненапечатанных элементов множества; пусть это x. Тогда он делится нацело на одно из чисел 2, 3, 5, и частное также принадлежит множеству. Значит, оно напечатано. Значит, x находится в одной из очередей и, следовательно, является в ней первым (меньшие напечатаны, а элементы очередей не напечатаны). Напечатав x, мы должны его изъять и добавить его кратные.

Длины очередей не превосходят числа напечатанных элементов.

Следующая задача связана с графами (к которым мы вернемся в "Разные алгоритмы на графах" ).

Пусть задано конечное множество, элементы которого называют вершина, а также некоторое множество упорядоченных пар вершин, называемых ребрами. В этом случае говорят, что задан ориентированный граф. Пару 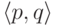называют ребром с началом p и концом q ; говорят также, что оно выходит из вершины p и входит в вершину q. Обычно вершины графа изображают точками, а ребра - стрелками, ведущими из начала в конец. (В соответствии с определением из данной вершины в данную ведет не более одного ребра ; возможны ребра, у которых начало совпадает с концом.)

6.2.6. Известно, что ориентированный граф связен, т.е. из любой вершины можно пройти в любую по ребрам. Кроме того, из каждой вершины выходит столько же ребер, сколько входит. Доказать, что существует замкнутый цикл, проходящий по каждому ребру ровно один раз. Составить алгоритм отыскания такого цикла.

Решение. Змеей будем называть непустую очередь из вершин, в которой любые две вершины соединены ребром графа (началом является та вершина, которая ближе к началу очереди). Стоящая в начале очереди вершина будет хвостом змеи, последняя - головой. На рисунке змея изобразится в виде цепи ребер графа, стрелки ведут от хвоста к голове. Добавление вершины в очередь соответствует росту змеи с головы, взятие вершины - отрезанию кончика хвоста.

Вначале змея состоит из единственной вершины. Далее мы следуем такому правилу:

while змея включает не все ребра do begin
| if из головы выходит не входящее в змею ребро then begin
| | удлинить змею этим ребром
| end else begin
| | {голова змеи в той же вершине, что и хвост}
| | отрезать конец хвоста и добавить его к голове
| | {"змея откусывает конец хвоста"}
| end;
end;

Докажем, что мы достигнем цели.

(1) Идя по змее от хвоста к голове, мы входим в каждую вершину столько же раз, сколько выходим. Так как в любую вершину входит столько же ребер, сколько выходит, то невозможность выйти означает, что голова змеи в той же точке, что и хвост.

(2) Змея не укорачивается, поэтому либо она охватит все ребра, либо, начиная с некоторого момента, будет иметь постоянную длину. Во втором случае змея будет бесконечно "скользить по себе". Это возможно, только если из всех вершин змеи не выходит неиспользованных ребер. В этом случае из связности следует, что змея проходит по всем ребрам.

Замечание по реализации на паскале. Вершинами графа будем считать числа 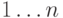. Для каждой вершины i будем хранить число Out[i] выходящих из нее ребер, а также номера Num[i][1],..., Num[i][Out[i]] тех вершин, куда эти ребра ведут. В процессе построения змеи будем выбирать первое свободное ребро. Тогда достаточно хранить для каждой вершины число выходящих из нее использованных ребер - это будут ребра, идущие в начале списка.

6.2.7. Доказать, что для всякого n существует последовательность нулей и единиц длины со следующим свойством: если "свернуть ее в кольцо" и рассмотреть все фрагменты длины n (их число равно ), то мы получим все возможные последовательности нулей и единиц длины n. Построить алгоритм отыскания такой последовательности, требующий не более 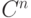действий для некоторой константы C.

Указание. Рассмотрим граф, вершинами которого являются последовательности нулей и единиц длины . Будем считать, что из вершины x ведет ребро в вершину y, если x может быть началом, а y - концом некоторой последовательности длины n. Тогда из каждой вершины входит и выходит два ребра. Цикл, проходящий по всем ребрам, и даст требуемую последовательность.

6.2.8. Реализовать k очередей с ограниченной суммарной длиной n, используя память 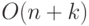[= не более 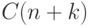для некоторой константы C ], причем каждая операция (кроме начальной, делающей все очереди пустыми) должна требовать ограниченного константой числа действий.

Решение. Действуем аналогично ссылочной реализации стеков: мы помним (для каждой очереди) первого, каждый участник очереди помнит следующего за ним (для последнего считается, что за ним стоит фиктивный элемент с номером 0 ). Кроме того, мы должны для каждой очереди знать последнего (если он есть) - иначе не удастся добавлять. Как и для стеков, отдельно есть цепь свободных ячеек. Заметим, что для пустой очереди информация о последнем элементе теряет смысл - но она и не используется при добавлении.

Содержание: array [1..n] of T;
Следующий: array [1..n] of 0..n;
Первый: array [1..k] of 0..n;
Последний: array [1..k] of 0..n;
Свободная : 0..n;

procedure Сделать_пустым;
| var i: integer;
begin
| for i := 1 to n-1 do begin
| | Следующий [i] := i + 1;
| end;
| Следующий [n] := 0;
| Свободная := 1;
| for i := 1 to k do begin
| | Первый [i]:=0;
| end;
end;

function Есть_место : boolean;
begin
| Есть_место := Свободная <> 0;
end;

function Пуста (номер_очереди: integer): boolean;
begin
| Пуста := Первый [номер_очереди] = 0;
end;

procedure Взять (var t: T; номер_очереди: integer);
| var перв: integer;
begin
| {not Пуста (номер_очереди)}
| перв := Первый [номер_очереди];
| t := Содержание [перв]
| Первый [номер_очереди] := Следующий [перв];
| Следующий [перв] := Свободная;
| Свободная := перв;
end;

procedure Добавить (t: T; номер_очереди: integer);
| var нов, посл: 1..n;
begin
| {Есть_место }
| нов := Свободная; Свободная := Следующий [Свободная];
| {из списка свободного места изъят номер нов}
| if Пуста (номер_очереди) then begin
| | Первый [номер_очереди] := нов;
| | Последний [номер_очереди] := нов;
| | Следующий [нов] := 0;
| | Содержание [нов] := t;
| end else begin
| | посл := Последний [номер_очереди];
| | {Следующий [посл] = 0 }
| | Следующий [посл] := нов;
| | Следующий [нов] := 0;
| | Содержание [нов] := t
| | Последний [номер_очереди] := нов;
| end;
end;

function Очередной (номер_очереди: integer): T;
begin
| Очередной := Содержание [Первый [номер_очереди]];
end;

6.2.9. Та же задача для деков вместо очередей.

Указание. Дек - структура симметричная, поэтому надо хранить ссылки в обе стороны (вперед и назад). При этом удобно к каждому деку добавить фиктивный элемент, замкнув его в кольцо, и точно такое же кольцо образовать из свободных позиций.

В следующей задаче дек используется для хранения вершин выпуклого многоугольника.

6.2.10. На плоскости задано n точек, пронумерованных слева направо (а при равных абсциссах - снизу вверх). Составить программу, которая строит многоугольник, являющийся их выпуклой оболочкой, за [= не более чем ] действий.

Решение. Будем присоединять точки к выпуклой оболочке одна за другой. Легко показать, что последняя присоединенная точка будет одной из вершин выпуклой оболочки. Эту вершину мы будем называть выделенной. Очередная присоединяемая точка видна из выделенной (почему?). Дополним наш многоугольник, выпустив из выделенной вершины "иглу", ведущую в присоединяемую точку. Получится вырожденный многоугольник, и остается ликвидировать в нем " впуклости".

Будем хранить вершины многоугольника в деке в порядке обхода его периметра по часовой стрелке. При этом выделенная вершина является началом и концом (головой и хвостом) дека. Присоединение "иглы" теперь состоит в добавлении присоединяемой вершины в голову и в хвост дека. Устранение впуклостей несколько более сложно. Назовем подхвостом и подподхвостом элементы дека, стоящие за его хвостом. Устранение впуклости у хвоста делается так:

while по дороге из хвоста в подподхвост  мы поворачиваем
| у подхвоста влево ("впуклость") do begin
| выкинуть подхвост из дека
end

Таким же способом устраняется впуклость у головы дека.

Замечание. Действия с подхвостом и подподхвостом не входят в определение дека, однако сводятся к небольшому числу манипуляций с деком (надо забрать три элемента с хвоста, сделать что надо и вернуть).

Еще одно замечание. Есть два вырожденных случая: если мы вообще не поворачиваем у подхвоста (т.е. три соседние вершины лежат на одной прямой) и если мы поворачиваем на 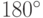(так бывает, если наш многоугольник есть двуугольник). В первом случае подхвост стоит удалить (чтобы в выпуклой оболочке не было лишних вершин), а во втором случае - обязательно оставить.