| Россия, Москва |
Контрастирование (редукция) нейронной сети
Сокращение описания "сверху вниз" - набор достаточного семейства наиболее значимых параметров
Метод исключения параметров "сверху вниз" с ортогонализацией
применим не
ко всяким функциям  , а только к таким, которые имеют вид:
, а только к таким, которые имеют вид:
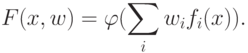
Достоинство метода - автоматический учет корреляции между  .
Рассмотрим устройства, вычисляющие функции
.
Рассмотрим устройства, вычисляющие функции
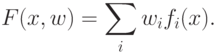
К ним относятся линейные сумматоры, квадратичные сумматоры и др.
Пусть заданы векторы данных:

Поставим задачу сокращения описания следующим образом: так определить
некоторое наименьшее возможное множество индексов 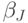 и набор
чисел
и набор
чисел 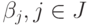 ,
чтобы норма отклонения
,
чтобы норма отклонения 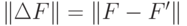 , где
, где  , не
превышала некоторой наперед заданной величины. Все функции
рассматриваются на конечном множестве
, не
превышала некоторой наперед заданной величины. Все функции
рассматриваются на конечном множестве 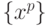 . Для любой функции
. Для любой функции 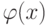 евклидова норма:
евклидова норма:
![\begin{align*}
\|\varphi\| =[\sum_p \varphi^2(x^p)]^{1/2}.
\end{align*}](/sites/default/files/tex_cache/1000ae8e4ef1c01e21f9ea71dd1c5825.png)
С каждой функцией  связан
связан  -мерный вектор
-мерный вектор  с компонентами
с компонентами 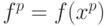 . Вектор
. Вектор  с координатами
с координатами 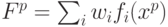 является линейной
комбинацией векторов
является линейной
комбинацией векторов 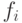 с координатами
с координатами 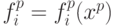 . Линейную оболочку
семейства векторов
. Линейную оболочку
семейства векторов 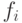 обозначим
обозначим 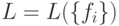 .
Построим в пространстве
.
Построим в пространстве  ортонормированный базис с помощью последовательной
ортогонализации
векторов
ортонормированный базис с помощью последовательной
ортогонализации
векторов 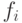 . Каждый следующий шаг ортогонализации выполним так,
чтобы
величина проекции
. Каждый следующий шаг ортогонализации выполним так,
чтобы
величина проекции  на новый вектор базиса была максимальной из
возможных.
Процесс ортогонализации продолжим, пока
на новый вектор базиса была максимальной из
возможных.
Процесс ортогонализации продолжим, пока  , где
, где 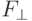 -
проекция
-
проекция  на построенную ортогональную систему. По окончании
процесса
полагаем
на построенную ортогональную систему. По окончании
процесса
полагаем 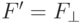 .
.

