| Россия, Москва |
Контрастирование (редукция) нейронной сети
Показатели значимости вычисляются в два этапа: сначала они оцениваются для одного вектора (примера), потом для всей выборки.
1. Для данного 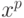 значимости
значимости 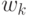 и
и  оцениваются как
оцениваются как
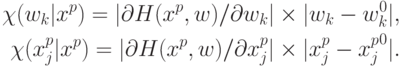
Здесь 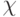 - вычисленные в линейном приближении абсолютные
величины изменения
- вычисленные в линейном приближении абсолютные
величины изменения  при сокращении описания. Оценка на всей выборке
при сокращении описания. Оценка на всей выборке 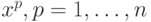 может
проводиться по-разному. Например, может использоваться одна из следующих
норм:
может
проводиться по-разному. Например, может использоваться одна из следующих
норм:
1. Сумма модулей:
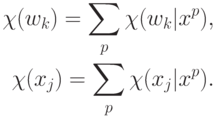
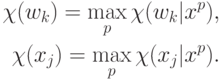
Часто приходится иметь дело с системой, которая меняет свои параметры
(например, в ходе обучения). Тогда к моменту принятия решения о значимости
может быть накоплена информация о частных производных  в разных
точках
в разных
точках 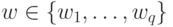 . Ее можно использовать следующим
образом.
. Ее можно использовать следующим
образом.
Обозначим угловыми скобками процедуру усреднения по множеству параметров 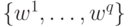 :
:
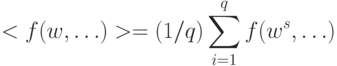
положим
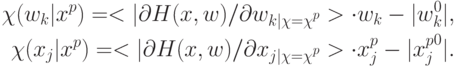
Усредняются абсолютные значения производных, а приращения берутся в тех
точках, в которых будет проводиться процедура сокращения описания.
Усреднение параметров  по нескольким значениям важно для
нелинейных
систем, в которых производные
по нескольким значениям важно для
нелинейных
систем, в которых производные  могут сильно меняться от точки к
точке.
могут сильно меняться от точки к
точке.
Главная задача при сокращении описания - сохранить качество работы
системы, оцениваемое с помощью  . Для этого требуется знать
назначение
системы и иметь способ оценки ее соответствия своему назначению.
. Для этого требуется знать
назначение
системы и иметь способ оценки ее соответствия своему назначению.
Возможен другой подход, не предполагающий никакого знания о способах оценки. Ставится задача сохранить описание, минимально изменяя функционирование системы. В этом случае роль оценки играет изменение выходного сигнала системы после сокращения.

