НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 15: Алгоритмические проблемы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: профессионал | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 33 студентам

| Поделиться |

Поддержать программу

Аннотация: В данной лекции рассматриваются понятия вычислимости, разрешимости, перечислимости и универсальных моделей вычислений. Рассмотрены алгоритмические проблемы, связанные с контекстно-свободными грамматиками, вводятся термины "массовая задача", "индивидуальная задача", "схема кодирования", "задача распознавания", "алгоритмическая проблема". Приведены практические примеры и задачи для самостоятельной проработки

Ключевые слова: модель вычислений, машина Тьюринга, множества, алгоритмическая, alphabetize, reject, encoding scheme, solvable, undecidable, unsolvability, разрешимые множества

Основная цель этой лекции - дать определения понятий, необходимых для математически строгой формулировки результатов следующих двух лекций. Для более подробного ознакомления с вычислимостью, разрешимостью, перечислимостью и универсальными моделями вычислений следует обратиться к какому-либо вводному курсу по теории алгоритмов, например [30, с. 93-106, 109-121] или [5,с. 8-20, 112-123]. В разделе 14.1 фиксируется конкретная модель вычислений - машина Тьюринга и даются определения (недетерминированной) машины Тьюринга, детерминированной машины Тьюринга и вычислимой функции. В разделе 14.2 определяются разрешимые и перечислимые множества. В разделе 14.3 вводятся термины "массовая задача", "индивидуальная задача", "схема кодирования", "задача распознавания", "алгоритмическая проблема". В 14.4* формулируется теорема о соответствии машин Тьюринга грамматикам типа 0, а также теорема о нормальной форме для грамматик типа 0. В разделе 14.5 формулируется известная неразрешимая проблема - проблема соответствий Поста. На сведEнии именно к этой алгоритмической проблеме основываются все доказательства неразрешимости в "Алгоритмически неразрешимые проблемы" , где рассматриваются алгоритмические проблемы, связанные с контекстно-свободными грамматиками.

14.1. Машины Тьюринга

Определение 14.1.1. Машиной Тьюринга называется семерка

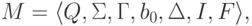
$M \peq \lalg Q , \Sigma , \Gamma , b_0 , \Delta , I , F \ralg ,$

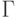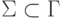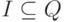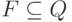где Q, $\Gamma$ и $\Delta$ - конечные множества, $\Sigma \subset \Gamma$ , $b_0 \in \Gamma \sminus \Sigma$ , $I \subseteq Q$ , $F \subseteq Q$ и

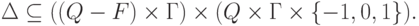
$\Delta \subseteq (( Q \sminus F ) \times \Gamma ) \times ( Q \times \Gamma \times \{ -1 , 0 , 1 \} ) .$

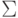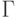Здесь Q - множество состояний $\Sigma$ - входной алфавит ( внешний алфавит ), $\Gamma$ - ленточный алфавит (tape alphabet), b₀ - бланк ( пробел, пустой символ, blank symbol), $\Delta$ - множество переходов, I - множество начальных состояний, F - множество заключительных состояний.

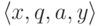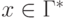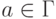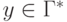Определение 14.1.2. Конфигурацией машины Тьюринга называется любая четверка $\lp x , q , a , y \rp$ , где $x \in \Gamma ^*$ , $q \in Q$ , $a \in \Gamma$ , $y \in \Gamma ^*$ .

Определение 14.1.3. Определим на множестве всех конфигураций машины Тьюринга M бинарное отношение 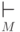$\myunderset{ M }{\vdash}$ ( такт работы ) следующим образом.

Если 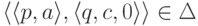$\lp \lp p , a \rp , \lp q , c , 0 \rp \rp \in \Delta$ , то

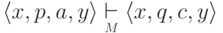
$\lp x , p , a , y \rp \myunderset{ M }{\vdash} \lp x , q , c , y \rp$

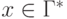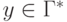для всех $x \in \Gamma ^*$ и $y \in \Gamma ^*$ .

Если $\lp \lp p , a \rp , \lp q , c , 1 \rp \rp \in \Delta$ , то

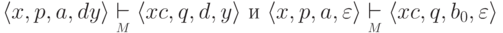
$\lp x , p , a , d y \rp \myunderset{ M }{\vdash} \lp x c , q , d , y \rp \rusand \lp x , p , a , \varepsilon \rp \myunderset{ M }{\vdash} \lp x c , q , b_0 , \varepsilon \rp$

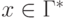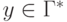для всех $x \in \Gamma ^*$ , $y \in \Gamma ^*$ и $d \in \Gamma$ .

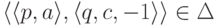Если $\lp \lp p , a \rp , \lp q , c , -1 \rp \rp \in \Delta$ , то

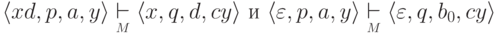
$\lp x d , p , a , y \rp \myunderset{ M }{\vdash} \lp x , q , d , c y \rp \rusand \lp \varepsilon , p , a , y \rp \myunderset{ M }{\vdash} \lp \varepsilon , q , b_0 , c y \rp$

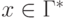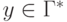для всех $x \in \Gamma ^*$ , $y \in \Gamma ^*$ и $d \in \Gamma$ .

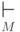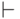Замечание 14.1.4. Если из контекста ясно, о какой машине Тьюринга идет речь, вместо $\myunderset{ M }{\vdash}$ будем писать просто $\vdash$ .

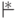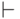Определение 14.1.5. Как и для МП-автомата, для машины Тьюринга бинарное отношение $\overstar{\vdash}$ определяется как рефлексивное, транзитивное замыкание отношения $\vdash$ .

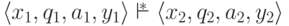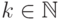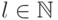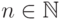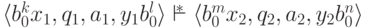Замечание 14.1.6. Если $\lp x_1 , q_1 , a_1 , y_1 \rp \overstar{\vdash} \lp x_2 , q_2 , a_2 , y_2 \rp$ , то для любых $k \in \mathbb{N}$ и $l \in \mathbb{N}$ найдутся такие $m \in \mathbb{N}$ и $n \in \mathbb{N}$ , что $\lp b_0 ^k x_1 , q_1 , a_1 , y_1 b_0 ^l \rp \overstar{\vdash} \lp b_0 ^m x_2 , q_2 , a_2 , y_2 b_0 ^n \rp$ .

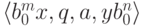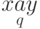Замечание 14.1.7. Конфигурацию $\lp b_0 ^m x , q , a , y b_0 ^n \rp$ иногда изображают сокращенно $x \underset{ q }{ a } y$ .

Замечание 14.1.8. Машины Тьюринга можно изображать в виде диаграмм. При этом каждое состояние обозначается кружком, а переход - стрелкой. Каждое начальное состояние распознается по ведущей в него короткой стрелке. Каждое заключительное состояние отмечается на диаграмме двойным кружком. Стрелка с пометкой a:ck, ведущая из p в q, показывает, что 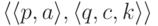$\lp \lp p , a \rp , \lp q , c , k \rp \rp$ является переходом данной машины Тьюринга. Обычно на диаграммах вместо чисел -1, 0, 1 (обозначающих движение влево, стояние на месте, движение вправо) используются буквы L, N, R соответственно.

Пример 14.1.9. Рассмотрим машину Тьюринга

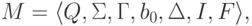
$M \peq \lalg Q , \Sigma , \Gamma , b_0 , \Delta , I , F \ralg ,$

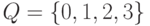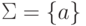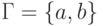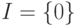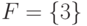где $Q \peq \{ 0 , 1 , 2 , 3 \}$ , $\Sigma \peq \{ a \}$ , $\Gamma \peq \{ a , b \}$ , $b_0 \peq b$ , $I \peq \{ 0 \}$ , $F \peq \{ 3 \}$ ,

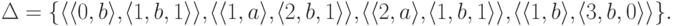
$\Delta \peq \{ \lp \lp 0 , b \rp \sqzcm \lp 1 , b , 1 \rp \rp \sqzcm \lp \lp 1 , a \rp \sqzcm \lp 2 , b , 1 \rp \rp \sqzcm \lp \lp 2 , a \rp \sqzcm \lp 1 , b , 1 \rp \rp \sqzcm \lp \lp 1 , b \rp \sqzcm \lp 3 , b , 0 \rp \rp \} .$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{0} \ar @`{+/l16mm/} [] ^{} \ar "1,2" ^{b:b\dr} & *=[o][F-]{1} \ar "2,2" <0.6mm> ^{a:b\dr} \ar "1,3" ^{b:b\dn} & *=[o][F=]{3} \\ % & *=[o][F-]{2} \ar "1,2" <0.6mm> ^{a:b\dr} & }$

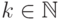Можно проверить, что для любого $k \in \mathbb{N}$ выполняется следующее: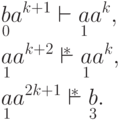

$\begin{align*} & \underset{ 0 }{ b } a ^{k+1} \vdash \underset{ 1 }{ a } a ^k ,\\ & \underset{ 1 }{ a } a ^{k+2} \overstar{\vdash} \underset{ 1 }{ a } a ^k ,\\ & \underset{ 1 }{ a } a ^{2k+1} \overstar{\vdash} \underset{ 3 }{ b } . \end{align*}$

Определение 14.1.10. Машина Тьюринга

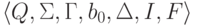
$\lalg Q , \Sigma , \Gamma , b_0 , \Delta , I , F \ralg$

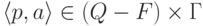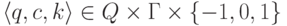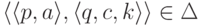называется детерминированной, если множество I содержит ровно один элемент и для каждой пары $\lp p , a \rp \in ( Q \sminus F ) \times \Gamma$ существует не более одной тройки $\lp q , c , k \rp \in Q \times \Gamma \times \{ -1 , 0 , 1 \}$ со свойством $\lp \lp p , a \rp , \lp q , c , k \rp \rp \in \Delta$ .

Пример 14.1.11 Машина Тьюринга из примера 14.1.9 является детерминированной.

Дальше >>

Математическая теория формальных языков

Математическая теория формальных языков

Алгоритмические проблемы

14.1. Машины Тьюринга

Вопросы и ответы

Студенты

Авторизоваться

Математическая теория формальных языков

Математическая теория формальных языков

Алгоритмические проблемы

14.1. Машины Тьюринга

Вопросы и ответы

Студенты