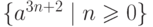НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 15: Алгоритмические проблемы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: профессионал | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 33 студентам

| Поделиться |

Поддержать программу

Упражнение 14.1.20. Рассмотрим детерминированную машину Тьюринга, изображенную на рисунке.

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{1} \ar @`{+/l16mm/} [] ^{} \ar "1,2" ^{b:b\dr} & *=[o][F-]{2} \ar "1,3" ^{a:b\dr} \ar "2,3" _{b:b\dn} & *=[o][F-]{3} \ar "1,4" ^{a:b\dr} \ar "2,3" ^{b:b\dn} & *=[o][F-]{4} \ar "1,5" ^{a:b\dr} \ar "2,3" ^{b:b\dn} & *=[o][F-]{5} \rloop{0,1} ^{a:b\dr} \ar "2,5" ^{b:b\dn} \\ % & & *=[o][F=]{6} & & *=[o][F=]{7} }$

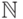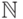Какую функцию из $\mathbb{N}$ в $\mathbb{N}$ она вычисляет?

Упражнение 14.1.21. Рассмотрим детерминированную машину Тьюринга, изображенную на рисунке.

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { % & *=[o][F-]{6} \rloop{0,1} ^{b:b\dr} \ar "1,3" ^{a:a\dr} & *=[o][F-]{7} \rloop{0,1} ^{a:a\dr} \ar "2,3" ^{b:a\dl} & & *=[o][F-]{1} \ar @`{+/l16mm/} [] ^{} \ar "1,6" ^{b:a\dr} & *=[o][F-]{2} \rloop{0,1} ^{a:a\dr} \ar "1,7" ^{b:b\dr} & *=[o][F-]{3} \rloop{0,1} ^{a:b\dr} \ar @/^4mm/ "3,2" ^{b:a\dl} \\ % & & *=[o][F-]{8} \rloop{0,-1} ^{a:a\dl} \ar "3,2" _{b:b\dl} & & & & \\ *=[o][F-]{5} \ar "1,2" ^{a:a\dr} \ar "4,2" _{b:b\dr} & *=[o][F-]{4} \rloop{0,-1} ^{b:b\dl} \ar "3,1" _{a:b\dl} & & & *=[o][F-]{10} \ar "4,7" ^{b:a\dr} & & \\ % & *=[o][F-]{9} \rloop{0,-1} ^{a:b\dl} \ar "3,5" ^{b:b\dr} & *=[o][F-]{15} \rloop{0,-1} ^{a:a\dl} \ar "4,5" ^{b:a\dr} & & *=[o][F-]{16} \rloop{0,1} ^{a:a\dr} \ar "4,7" ^{b:b\dr} & & *=[o][F-]{11} \rloop{0,1} ^{b:b\dr} \ar "5,6" ^{a:a\dl} \\ % & & & *=[o][F-]{14} \rloop{0,-1} ^{b:b\dl} \ar "4,3" ^(0.3){a:a\dl} & *=[o][F-]{13} \ar "5,4" ^{b:b\dl} \ar "6,4" ^{a:b\dl} & *=[o][F-]{12} \ar "5,5" ^{b:a\dl} \ar "6,7" ^(0.3){a:b\dr} & \\ % & & & *=[o][F-]{17} \ar "4,2" ^{a:b\dl} \ar "6,7" ^{b:b\dr} & & & *=[o][F-]{18} \rloop{0,1} ^{b:b\dr} \ar "7,7" ^{a:b\dn} \\ % & & & & & & *=[o][F=]{19} }$

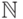Какую функцию из $\mathbb{N} \times \mathbb{N}$ в $\mathbb{N}$ она вычисляет?

14.2. Разрешимые и перечислимые множества

Определение 14.2.1. Говорят, что детерминированная машина Тьюринга

$\lalg Q , \Sigma , \Gamma , b_0 , \Delta , \{ \qinitial \} , \{ \qaccept , \qreject \} \ralg$

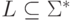с выделенным состоянием q_a разрешает (decides) язык $L \subseteq \Sigma ^*$ , если

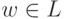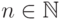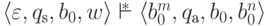1) для каждого слова $w \in L$ найдутся такие $m \in \mathbb{N}$ и $n \in \mathbb{N}$ , что $\lp \varepsilon , \qinitial , b_0 , w \rp \overstar{\vdash} \lp b_0 ^m , \qaccept , b_0 , b_0 ^n \rp$ ;

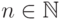2) для каждого слова $w \in \Sigma ^* \sminus L$ найдутся такие $m \in \mathbb{N}$ и $n \in \mathbb{N}$ , что $\lp \varepsilon , \qinitial , b_0 , w \rp \overstar{\vdash} \lp b_0 ^m , \qreject , b_0 , b_0 ^n \rp$ . Состояние q_a называется допускающим ( принимающим, accept state), состояние q_r называется отвергающим ( непринимающим, (reject state).

Пример 14.2.2. Рассмотрим детерминированную машину Тьюринга

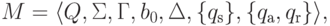
$M \peq \lalg Q , \Sigma , \Gamma , b_0 , \Delta , \{ \qinitial \} , \{ \qaccept , \qreject \} \ralg ,$

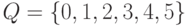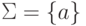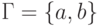где $Q = \{ 0 , 1 , 2 , 3 , 4 , 5 \}$ , $\Sigma = \{ a \}$ , $\Gamma = \{ a , b \}$ , b_0 = b

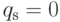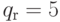, $\qinitial = 0$ , $\qaccept = 4$ , $\qreject = 5$ и

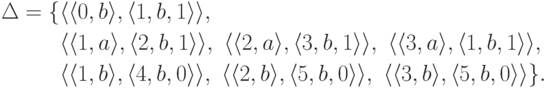
$\begin{align*} {} \Delta &= \{ \lp \lp 0 , b \rp , \lp 1 , b , 1 \rp \rp ,\ \\ &\hphantom{ {} = {} \{ } %\} \lp \lp 1 , a \rp , \lp 2 , b , 1 \rp \rp ,\ \lp \lp 2 , a \rp , \lp 3 , b , 1 \rp \rp ,\ \lp \lp 3 , a \rp , \lp 1 , b , 1 \rp \rp ,\ \\ &\hphantom{ {} = {} \{ } %\} \lp \lp 1 , b \rp , \lp 4 , b , 0 \rp \rp ,\ \lp \lp 2 , b \rp , \lp 5 , b , 0 \rp \rp ,\ \lp \lp 3 , b \rp , \lp 5 , b , 0 \rp \rp \} . \end{align*}$

$\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle \xymatrix { *=[o][F-]{0} \ar @`{+/l16mm/} [] ^{} \ar "1,2" ^{b:b\dr} & *=[o][F-]{1} \ar "1,3" ^{a:b\dr} \ar "2,2" ^{b:b\dn} & *=[o][F-]{2} \ar "1,4" ^{a:b\dr} \ar "2,4" _{b:b\dn} & *=[o][F-]{3} \ar `ul^l{+/u7mm/}`l^dl{[0,-2]}_{a:b\dr} "1,2" \ar "2,4" ^{b:b\dn} \\ % & *=[o][F=]{4} & & *=[o][F=]{5} }$

Эта машина Тьюринга разрешает язык $\{ a^{3n} \mid n \in \mathbb{N} \}$ .

Определение 14.2.3. Язык L над алфавитом 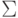$\Sigma$ называется разрешимым или рекурсивным (decidable, recursive), если существует детерминированная машина Тьюринга

$\lalg Q , \Sigma , \Gamma , b_0 , \Delta , \{ \qinitial \} , \{ \qaccept , \qreject \} \ralg$

(с выделенным состоянием q_a ), которая разрешает язык L.

Определение 14.2.4. Говорят, что машина Тьюринга

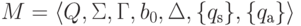
$M \peq \lalg Q , \Sigma , \Gamma , b_0 , \Delta , \{ \qinitial \} , \{ \qaccept \} \ralg$

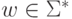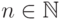
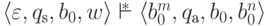допускает ( принимает, accepts) слово $w \in \Sigma ^*$ , если для некоторых $m \in \mathbb{N}$ и $n \in \mathbb{N}$ $\lp \varepsilon , \qinitial , b_0 , w \rp \overstar{\vdash} \lp b_0 ^m , \qaccept , b_0 , b_0 ^n \rp$ .

Определение 14.2.5. Язык, допускаемый машиной Тьюринга M, - это язык, состоящий из всех допускаемых данной машиной Тьюринга слов.

Определение 14.2.6. Язык называется перечислимым ( рекурсивно перечислимым, полуразрешимым, recursively enumerable), если существует детерминированная машина Тьюринга, допускающая этот язык.

Замечание 14.2.7. В определении 14.2.6 можно отбросить требование детерминированности машины Тьюринга.

Теорема 14.2.8. Каждый разрешимый язык является перечислимым.

Доказательство. Пусть дана машина Тьюринга

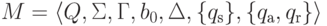
$M \peq \lalg Q , \Sigma , \Gamma , b_0 , \Delta , \{ \qinitial \} , \{ \qaccept , \qreject \} \ralg$

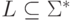с выделенным состоянием q_a, которая разрешает язык $L \subseteq \Sigma ^*$ . Тогда машина Тьюринга

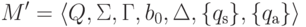
$M' \peq \lalg Q , \Sigma , \Gamma , b_0 , \Delta , \{ \qinitial \} , \{ \qaccept \} \ralg$

допускает язык L.

Пример 14.2.9. Если в машине Тьюринга из примера 14.1.15 заменить переход $\lp \lp 6 , a \rp , \lp 6 , a , -1 \rp \rp$ на $\lp \lp 6 , a \rp , \lp 6 , b , -1 \rp \rp$ , то получится машина Тьюринга, допускающая язык $\{ a^{n^2} \mid n \in \mathbb{N} \}$ . Следовательно, этот язык является перечислимым. Можно доказать, что он даже является разрешимым.

Теорема 14.2.10. Существует такая машина Тьюринга над однобуквенным алфавитом 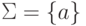$\Sigma = \{ a \}$ , что язык, допускаемый этой машиной Тьюринга, неразрешим.

Доказательство. Доказательство существования перечислимого неразрешимого множества можно найти, например, в [31, 9.2].

Упражнение 14.2.11. Найти детерминированную машину Тьюринга с входным алфавитом {a}, разрешающую язык 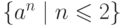$\{ a^{n} \mid n \leq 2 \}$ .

Упражнение 14.2.12. Найти детерминированную машину Тьюринга с входным алфавитом {a}, допускающую язык $\{ a^{3n+2} \mid n \geq 0 \}$

Дальше >>

Математическая теория формальных языков

Математическая теория формальных языков

Алгоритмические проблемы

14.2. Разрешимые и перечислимые множества

Вопросы и ответы

Студенты

Авторизоваться

Математическая теория формальных языков

Математическая теория формальных языков

Алгоритмические проблемы

14.2. Разрешимые и перечислимые множества

Вопросы и ответы

Студенты