|
Упражнение 2.1.25 |
Инспектор
Вы можете этот курс.
Опубликован: 09.07.2007 | Уровень: профессионал | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова
Лекция 15:
Алгоритмические проблемы
14.5. Проблема соответствий Поста
Определение 14.5.1. Постовской системой соответствия
над алфавитом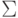 
называется упорядоченная
пара конечных последовательностей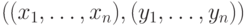 
,
где 
и 
для всех i.
Замечание 14.5.2.
Систему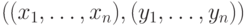
иногда изображают в виде
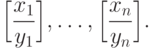
Определение 14.5.3. Решением (match)
постовской системы соответствия ((x1,...,xn),(y1,...,yn))
называется непустая последовательность индексов 
,
удовлетворяющая условию
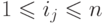для каждого j.Пример 14.5.4.
Пусть 
.
Рассмотрим постовскую систему соответствия
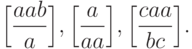
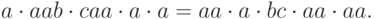
Упражнение 14.5.5.
Пусть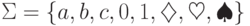 
.
Существует ли решение у постовской системы соответствия
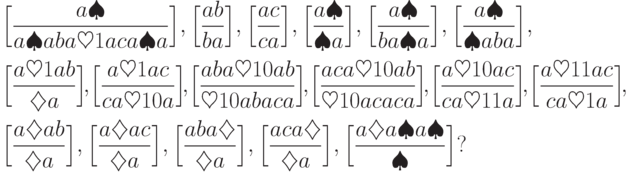
Определение 14.5.6. Проблемой соответствий Поста (Post correspondence problem) называется проблема нахождения алгоритма, выясняющего для каждой постовской системы соответствия, существует ли решение этой системы.
Теорема 14.5.7. Пусть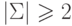 
. Тогда не существует алгоритма, позволяющего по произвольной
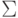постовской системе соответствия над алфавитом узнать, имеет ли она решение.
( Другими словами,
проблема соответствий Поста неразрешима.)
Доказательство можно найти в [ХопМот, 9.4].
Упражнение 14.5.8.
Существует ли решение у постовской системы соответствия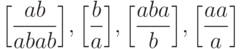 
?
Упражнение 14.5.9.
Существует ли решение у постовской системы соответствия 
?
Упражнение 14.5.10.
Существует ли решение у постовской системы соответствия 
?
Упражнение 14.5.11.
Существует ли решение у постовской системы соответствия 
?
Упражнение 14.5.12.
Существует ли решение у постовской системы соответствия 
?
Упражнение 14.5.13.
Существует ли решение у постовской системы соответствия 
?
Упражнение 14.5.14.
Существует ли решение у постовской системы соответствия 
?
Упражнение 14.5.15. Существует ли постовская система соответствия, имеющая ровно одно решение?
